47 8.4 Quantitative Chemical Analysis
Learning Objectives
By the end of this section, you will be able to:
- Perform Gravimetric Analysis
- Relate Gravimetric Analysis to Reaction Stoichiometry
- Perform a Combustion Analysis
Gravimetric Analysis
Gravimetric Analysis
A gravimetric analysis is one in which a sample is subjected to some treatment that causes a change in the physical state of the analyte that permits its separation from the other components of the sample. Mass measurements of the sample, the isolated analyte, or some other component of the analysis system, used along with the known stoichiometry of the compounds involved, permit calculation of the analyte concentration. Gravimetric methods were the first techniques used for quantitative chemical analysis, and they remain important tools in the modern chemistry laboratory.
The required change of state in a gravimetric analysis may be achieved by various physical and chemical processes. For example, the moisture (water) content of a sample is routinely determined by measuring the mass of a sample before and after it is subjected to a controlled heating process that evaporates the water. Also common are gravimetric techniques in which the analyte is subjected to a precipitation reaction of the sort described earlier in this chapter. The precipitate is typically isolated from the reaction mixture by filtration, carefully dried, and then weighed (Figure 2). The mass of the precipitate may then be used, along with relevant stoichiometric relationships, to calculate analyte concentration.

Example 2
Gravimetric Analysis
A 0.4550-g solid mixture containing MgSO4 is dissolved in water and treated with an excess of Ba(NO3)2, resulting in the precipitation of 0.6168 g of BaSO4.
What is the concentration (percent) of MgSO4 in the mixture?
Solution
The plan for this calculation is similar to others used in stoichiometric calculations, the central step being the connection between the moles of BaSO4 and MgSO4 through their stoichiometric factor. Once the mass of MgSO4 is computed, it may be used along with the mass of the sample mixture to calculate the requested percentage concentration.
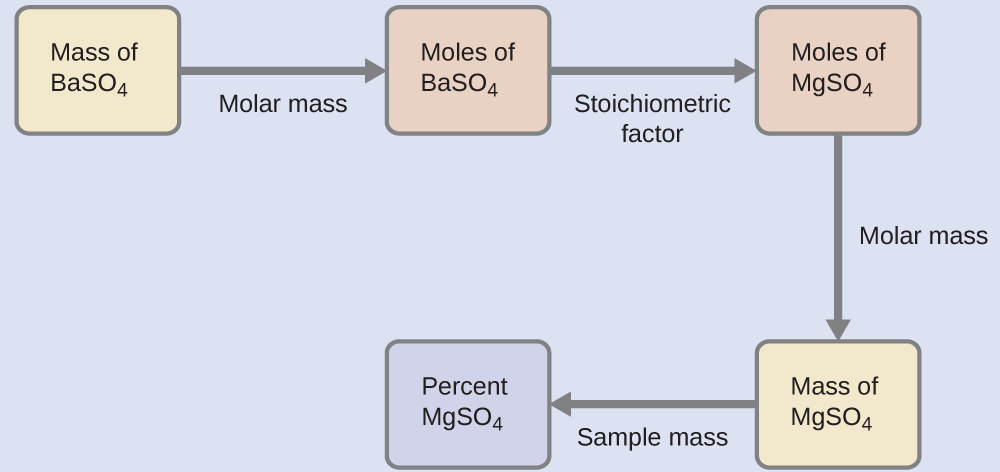
The mass of MgSO4 that would yield the provided precipitate mass is
[latex]0.6168 \;\rule[0.5ex]{3.75em}{0.1ex}\hspace{-3.75em}\text{g BaSO}_4 \times \frac{1 \;\rule[0.25ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{mol BaSO}_4}{233.43 \;\rule[0.25ex]{2.75em}{0.1ex}\hspace{-2.75em}\text{g BaSO}_4} \times \frac{1 \;\rule[0.25ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{mol MgSO}_4}{1\;\rule[0.25ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{mol BaSO}_4} \times \frac{120.37 \;\text{g MgSO}_4}{1 \;\rule[0.25ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{mol MgSO}_4} = 0.3181 \;\text{g MgSO}_4[/latex]
The concentration of MgSO4 in the sample mixture is then calculated to be:
[latex]\begin{array}{rl @{{}={}} l}\text{percent MgSO}_4 & = \frac{\text{mass MgSO}_4}{\text{mass sample}} \times 100\% \\[0.5em] & = \frac{0.3181 \;\text{g}}{0.4550 \;\text{g}} \times 100\%\\[0.5em] & = 69.91\% \end{array}[/latex]
Check Your Learning
What is the percent of chloride ion in a sample if 1.1324 g of the sample produces 1.0881 g of AgCl when treated with excess Ag+?
Answer:
23.76%
Example 3
Gravimetric Analysis – No Balanced Chemical Equation Given
If 1.404 g of zinc chloride is dissolved in 350. mL of 0.030 M solution of silver nitrate and a white precipitate formed, how many grams of white precipitate can you collect?
Solution
First, write out and balance the chemical reaction starting with the reactants given (zinc chloride and silver nitrate):
[latex]\text{ZnCl}_{2}(s) + \text{2 AgNO}_{3}(aq) \longrightarrow \text{2 AgCl}(?) + \text{Zn(NO}_{3}\text{)}_2(?)[/latex]
Since this is a precipitation reaction, use the solubility rules to determine which of the two products will be insoluble (s):
[latex]\text{ZnCl}_{2}(s) + \text{2 AgNO}_{3}(aq) \longrightarrow \text{2 AgCl}(s) + \text{Zn(NO}_{3}\text{)}_2(aq)[/latex]
Compute the provided molar amounts of reactants, and then compare these amounts to the balanced equation to identify the limiting reactant:
[latex]1.404 \;\rule[0.5ex]{3.25em}{0.1ex}\hspace{-3.25em}\text{g ZnCl}_2 \times \frac{1 \;\rule[0.5ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{mol ZnCl}_2}{136.28 \;\rule[0.5ex]{2.75em}{0.1ex}\hspace{-2.75em}\text{g ZnCl}_2} \times \frac{2 \;\rule[0.5ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{mol AgCl}}{1\;\rule[0.5ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{mol ZnCl}_2} = 0.02060 \;\text{mol AgCl}[/latex]
[latex]350. \;\rule[0.5ex]{4.25em}{0.1ex}\hspace{-4.25em}\text{mL AgNO}_3 \times \frac{1 \;\rule[0.5ex]{3.75em}{0.1ex}\hspace{-3.75em}\text{L AgNO}_3}{1 000 \;\rule[0.5ex]{3.75em}{0.1ex}\hspace{-3.75em}\text{mL AgNO}_3} \times \frac{0.030 \;\rule[0.5ex]{4.25em}{0.1ex}\hspace{-4.25em}\text{mol AgNO}_3}{1 \;\rule[0.5ex]{3.75em}{0.1ex}\hspace{-3.75em}\text{L AgNO}_3} \times \frac{2 \;\text{mol AgCl}}{2 \;\rule[0.5ex]{4.25em}{0.1ex}\hspace{-4.25em}\text{mol AgNO}_3} = 0.0105 \;\text{mol AgCl}[/latex]
Silver nitrate produces the least amount of silver chloride, so it is the limiting reactant. Use that molar amount to continue the calculation:
[latex]0.0105 \;\rule[0.5ex]{3.75em}{0.1ex}\hspace{-3.75em}\text{mol AgCl} \times \frac{143.32 \;\rule[0.5ex]{3.75em}{0.1ex}\hspace{-3.75em}\text{g AgCl}}{1 \;\text{mol AgCl}} = 1.50 \;\text{g AgCl}[/latex]
Check Your Learning
If you started with 33.52 g of silver nitrate and added that to 700 mL of a 0.25 M solution of sodium phosphate, how many grams of the white precipitate are formed?
Answer:
27.5 g Ag3PO4(s) is formed due to AgNO3 being the limiting reactant
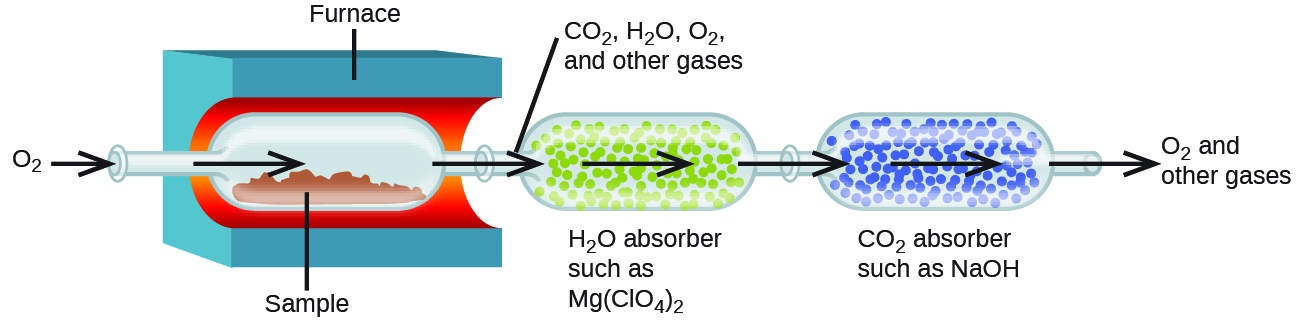
The elemental composition of hydrocarbons and related compounds may be determined via a gravimetric method known as combustion analysis. In a combustion analysis, a weighed sample of the compound is heated to a high temperature under a stream of oxygen gas, resulting in its complete combustion to yield gaseous products of known identities. The complete combustion of hydrocarbons, for example, will yield carbon dioxide and water as the only products. The gaseous combustion products are swept through separate, preweighed collection devices containing compounds that selectively absorb each product (Figure 3). The mass increase of each device corresponds to the mass of the absorbed product and may be used in an appropriate stoichiometric calculation to derive the mass of the relevant element.
Example 4
Combustion Analysis
Polyethylene is a hydrocarbon polymer used to produce food-storage bags and many other flexible plastic items. A combustion analysis of a 0.00126-g sample of polyethylene yields 0.00394 g of CO2 and 0.00161 g of H2O. What is the empirical formula of polyethylene?
Solution
The primary assumption in this exercise is that all the carbon in the sample combusted is converted to carbon dioxide, and all the hydrogen in the sample is converted to water:
Note that a balanced equation is not necessary for the task at hand. To derive the empirical formula of the compound, only the subscripts x and y are needed.
First, calculate the molar amounts of carbon and hydrogen in the sample, using the provided masses of the carbon dioxide and water, respectively. With these molar amounts, the empirical formula for the compound may be written as described in the previous chapter of this text. An outline of this approach is given in the following flow chart:
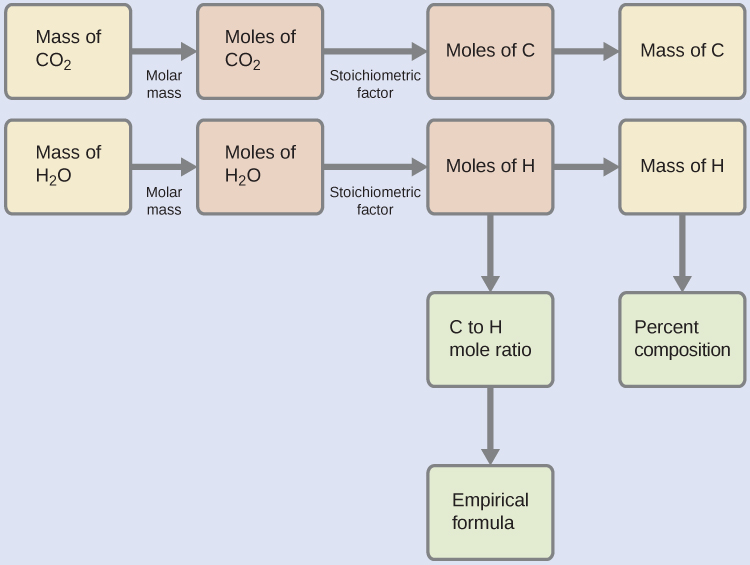
The empirical formula for the compound is then derived by identifying the smallest whole-number multiples for these molar amounts. The H-to-C molar ratio is
and the empirical formula for polyethylene is CH2.
Check Your Learning
A 0.00215-g sample of polystyrene, a polymer composed of carbon and hydrogen, produced 0.00726 g of CO2 and 0.00148 g of H2O in a combustion analysis. What is the empirical formula for polystyrene?
Answer:
CH
Key Concepts and Summary (*Note: This Chapter Summary and Chapter Practice Includes Titrations, which has been moved to Ch. 9.) Kindly disregard Titration problems and solutions until the next chapter)
The stoichiometry of chemical reactions may serve as the basis for quantitative chemical analysis methods. Titrations involve measuring the volume of a titrant solution required to completely react with a sample solution. This volume is then used to calculate the concentration of analyte in the sample using the stoichiometry of the titration reaction. Gravimetric analysis involves separating the analyte from the sample by a physical or chemical process, determining its mass, and then calculating its concentration in the sample based on the stoichiometry of the relevant process. Combustion analysis is a gravimetric method used to determine the elemental composition of a compound by collecting and weighing the gaseous products of its combustion.
Chemistry End of Chapter Exercises
- A sample of gallium bromide, GaBr2, weighing 0.165 g was dissolved in water and treated with silver nitrate, AgNO3, resulting in the precipitation of 0.299 g AgBr. Use these data to compute the %Ga (by mass) GaBr2.
- The principal component of mothballs is naphthalene, a compound with a molecular mass of about 130 amu, containing only carbon and hydrogen. A 3.000-mg sample of naphthalene burns to give 10.3 mg of CO2. Determine its empirical and molecular formulas.
- A 0.025-g sample of a compound composed of boron and hydrogen, with a molecular mass of ~28 amu, burns spontaneously when exposed to air, producing 0.063 g of B2O3. What are the empirical and molecular formulas of the compound?
- Sodium bicarbonate (baking soda), NaHCO3, can be purified by dissolving it in hot water (60 °C), filtering to remove insoluble impurities, cooling to 0 °C to precipitate solid NaHCO3, and then filtering to remove the solid, leaving soluble impurities in solution. Any NaHCO3 that remains in solution is not recovered. The solubility of NaHCO3 in hot water of 60 °C is 164 g/L. Its solubility in cold water of 0 °C is 69 g/L. What is the percent yield of NaHCO3 when it is purified by this method?
- What mass of Ca(OH)2 will react with 25.0 g of propionic acid to form the preservative calcium propionate according to the equation?
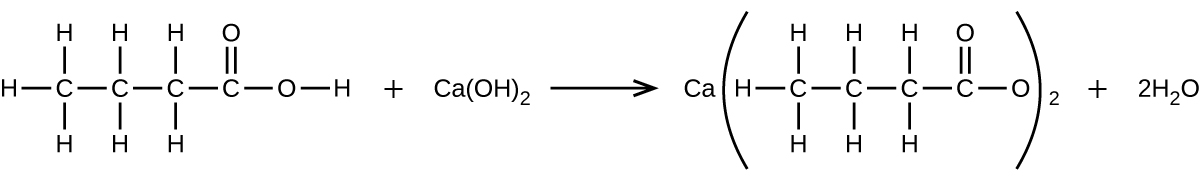
Glossary
- analyte
- chemical species of interest
- combustion analysis
- gravimetric technique used to determine the elemental composition of a compound via the collection and weighing of its gaseous combustion products
- gravimetric analysis
- quantitative chemical analysis method involving the separation of an analyte from a sample by a physical or chemical process and subsequent mass measurements of the analyte, reaction product, and/or sample
- quantitative analysis
- the determination of the amount or concentration of a substance in a sample
Solutions
Answers to Chemistry End of Chapter Exercises
1. 22.4%
3. The empirical formula is BH3. The molecular formula is B2H6.

