78 16.4 Equilibrium Calculations

Learning Objectives

By the end of this section, you will be able to:
  • Write equations representing changes in concentration and pressure for chemical species in equilibrium systems
  • Use algebra to perform various types of equilibrium calculations

We know that at equilibrium, the value of the reaction quotient of any reaction is equal to its equilibrium constant. Thus, we can use the mathematical expression for Q to determine a number of quantities associated with a reaction at equilibrium or approaching equilibrium. While we have learned to identify in which direction a reaction will shift to reach equilibrium, we want to extend that understanding to quantitative calculations. We do so by evaluating the ways that the concentrations of products and reactants change as a reaction approaches equilibrium, keeping in mind the stoichiometric ratios of the reaction. This algebraic approach to equilibrium calculations will be explored in this section.

Changes in concentrations or pressures of reactants and products occur as a reaction system approaches equilibrium. In this section we will see that we can relate these changes to each other using the coefficients in the balanced chemical equation describing the system. We use the decomposition of ammonia as an example.

On heating, ammonia reversibly decomposes into nitrogen and hydrogen according to this equation:

[latex]2\text{NH}_3(g)\;{\rightleftharpoons}\;\text{N}_2(g)\;+\;3\text{H}_2(g)[/latex]

If a sample of ammonia decomposes in a closed system and the concentration of N2 increases by 0.11 M, the change in the N2 concentration, Δ[N2], the final concentration minus the initial concentration, is 0.11 M. The change is positive because the concentration of N2 increases.

The change in the H2 concentration, Δ[H2], is also positive—the concentration of H2 increases as ammonia decomposes. The chemical equation tells us that the change in the concentration of H2 is three times the change in the concentration of N2 because for each mole of N2 produced, 3 moles of H2 are produced.

[latex]\begin{array}{rl @{{}={}} l} {\Delta}[\text{H}_2] & = 3\;\times\;{\Delta}[\text{N}_2] \\[0.5em] & = 3\;\times\;(0.11\;M) \\[0.5em] & = 0.33\;M\end{array}[/latex]

The change in concentration of NH3, Δ[NH3], is twice that of Δ[N2]; the equation indicates that 2 moles of NH3 must decompose for each mole of N2 formed. However, the change in the NH3 concentration is negative because the concentration of ammonia decreases as it decomposes.

[latex]{\Delta}[\text{NH}_3] = -2\;\times\;{\Delta}[\text{N}_2] = -2\;\times\;(0.11\;M) = -0.22\;M[/latex]

We can relate these relationships directly to the coefficients in the equation

[latex]\begin{array}{ccccc} 2\text{NH}_3(g) & {\rightleftharpoons} & \text{N}_2(g) & + & 3\text{H}_2(g) \\[0.5em] {\Delta}[\text{NH}_3] = -2\;\times\;{\Delta}[\text{N}_2] & & {\Delta}[\text{N}_2] = 0.11\;M & & {\Delta}[\text{H}_2] = 3\;\times\;{\Delta}[\text{N}_2] \end{array}[/latex]

Note that all the changes on one side of the arrows are of the same sign and that all the changes on the other side of the arrows are of the opposite sign.

If we did not know the magnitude of the change in the concentration of N2, we could represent it by the symbol x.

[latex]{\Delta}[\text{N}_2] = x[/latex]

The changes in the other concentrations would then be represented as:

[latex]{\Delta}[\text{H}_2] = 3\;\times\;{\Delta}[\text{N}_2] = 3x[/latex]
[latex]{\Delta}[\text{NH}_3] = -2\;\times\;{\Delta}[\text{N}_2] = -2x[/latex]

The coefficients in the Δ terms are identical to those in the balanced equation for the reaction.

[latex]\begin{array}{ccccc} 2\text{NH}_3(g) & {\rightleftharpoons} & \text{N}_2(g) & + & 3\text{H}_2(g) \\[0.5em] -2x & & x & & 3x \end{array}[/latex]

The simplest way for us to find the coefficients for the concentration changes in any reaction is to use the coefficients in the balanced chemical equation. The sign of the coefficient is positive when the concentration increases; it is negative when the concentration decreases.

Example 1

Determining Relative Changes in Concentration
Complete the changes in concentrations for each of the following reactions.

(a) [latex]\begin{array}{lcccc} \text{C}_2\text{H}_2(g) & + & 2\text{Br}_2(g) & {\rightleftharpoons} & \text{C}_2\text{H}_2\text{Br}_4(g) \\[0.5em] x & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} \end{array}[/latex]

 

(b) [latex]\begin{array}{lcccc} \text{I}_2(aq) & + & \text{I}^{-}(aq) & {\rightleftharpoons} & \text{I}_3^{\;\;-}(aq) \\[0.5em] \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} & & x \end{array}[/latex]

 

(c) [latex]\begin{array}{lcccccc} \text{C}_3\text{H}_8(g) & + & 5\text{O}_2(g) & {\rightleftharpoons} & 3\text{CO}_2(g) & + & 4\text{H}_2\text{O}(g) \\[0.5em] x & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} \end{array}[/latex]

 

Solution
(a) [latex]\begin{array}{lcccc} \text{C}_2\text{H}_2(g) & + & 2\text{Br}_2(g) & {\rightleftharpoons} & \text{C}_2\text{H}_2\text{Br}_4(g) \\[0.5em] x & & 2x & & -x \end{array}[/latex]

 

(b) [latex]\begin{array}{lcccc} \text{I}_2(aq) & + & \text{I}^{-}(aq) & {\rightleftharpoons} & \text{I}_3^{\;\;-}(aq) \\[0.5em] -x & & -x & & x \end{array}[/latex]

 

(c) [latex]\begin{array}{lcccccc} \text{C}_3\text{H}_8(g) & + & 5\text{O}_2(g) & {\rightleftharpoons} & 3\text{CO}_2(g) & + & 4\text{H}_2\text{O}(g) \\[0.5em] x & & 5x & & -3x & & -4x \end{array}[/latex]

 

Check Your Learning
Complete the changes in concentrations for each of the following reactions:

(a) [latex]\begin{array}{lcccc} 2\text{SO}_2(g) & + & \text{O}_2(g) & {\rightleftharpoons} & 2\text{SO}_3(g) \\[0.5em] \rule[0ex]{2.5em}{0.1ex} & & x & & \rule[0ex]{2.5em}{0.1ex} \end{array}[/latex]

 

(b) [latex]\begin{array}{lcc} \text{C}_4\text{H}_8(g) & {\rightleftharpoons} & 2\text{C}_2\text{H}_4(g) \\[0.5em] \rule[0ex]{2.5em}{0.1ex} & & -2x \end{array}[/latex]

 

(c) [latex]\begin{array}{lcccccc} 4\text{NH}_3(g) & + & 7\text{H}_2\text{O}(g) & {\rightleftharpoons} & 4\text{NO}_2(g) & + & 6\text{H}_2\text{O}(g) \\[0.5em] \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} \end{array}[/latex]

Answer:

(a) 2x, x, −2x; (b) x, −2x; (c) 4x, 7x, −4x, −6x or −4x, −7x, 4x, 6x

Calculations Involving Equilibrium Concentrations

Because the value of the reaction quotient of any reaction at equilibrium is equal to its equilibrium constant, we can use the mathematical expression for Qc (i.e., the law of mass action) to determine a number of quantities associated with a reaction at equilibrium. It may help if we keep in mind that Qc = Kc (at equilibrium) in all of these situations and that there are only three basic types of calculations:

  1. Calculation of an equilibrium constant. If concentrations of reactants and products at equilibrium are known, the value of the equilibrium constant for the reaction can be calculated.
  2. Calculation of missing equilibrium concentrations. If the value of the equilibrium constant and all of the equilibrium concentrations, except one, are known, the remaining concentration can be calculated.
  3. Calculation of equilibrium concentrations from initial concentrations. If the value of the equilibrium constant and a set of concentrations of reactants and products that are not at equilibrium are known, the concentrations at equilibrium can be calculated.

A similar list could be generated using QP, KP, and partial pressure. We will look at solving each of these cases in sequence.

Calculation of an Equilibrium Constant

Since the law of mass action is the only equation we have to describe the relationship between Kc and the concentrations of reactants and products, any problem that requires us to solve for Kc must provide enough information to determine the reactant and product concentrations at equilibrium. Armed with the concentrations, we can solve the equation for Kc, as it will be the only unknown.

Example 2 showed us how to determine the equilibrium constant of a reaction if we know the concentrations of reactants and products at equilibrium. The following example shows how to use the stoichiometry of the reaction and a combination of initial concentrations and equilibrium concentrations to determine an equilibrium constant. This technique, commonly called an ICE chart—for Initial, Change, and Equilibrium–will be helpful in solving many equilibrium problems. A chart is generated beginning with the equilibrium reaction in question. Underneath the reaction the initial concentrations of the reactants and products are listed—these conditions are usually provided in the problem and we consider no shift toward equilibrium to have happened. The next row of data is the change that occurs as the system shifts toward equilibrium—do not forget to consider the reaction stoichiometry as described in a previous section of this chapter. The last row contains the concentrations once equilibrium has been reached.

Example 2

Calculation of an Equilibrium Constant
Iodine molecules react reversibly with iodide ions to produce triiodide ions.

[latex]\text{I}_2(aq)\;+\;\text{I}^{-}(aq)\;{\rightleftharpoons}\;\text{I}_3^{\;\;-}(aq)[/latex]

If a solution with the concentrations of I2 and I− both equal to 1.000 × 10−3M before reaction gives an equilibrium concentration of I2 of 6.61 × 10−4M, what is the equilibrium constant for the reaction?

Solution
We will begin this problem by calculating the changes in concentration as the system goes to equilibrium. Then we determine the equilibrium concentrations and, finally, the equilibrium constant. First, we set up a table with the initial concentrations, the changes in concentrations, and the equilibrium concentrations using −x as the change in concentration of I2.
This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following in the first column: Initial concentration ( M ), Change ( M ), Equilibrium concentration ( M ). The second column has the header, “I subscript 2 plus sign I superscript negative sign equilibrium arrow I subscript 3 superscript negative sign.” Under the second column is a subgroup of three rows and three columns. The first column has the following: 1.000 times 10 to the negative third power, negative x, [ I subscript 2 ] subscript i minus x. The second column has the following: 1.000 times 10 to the negative third power, negative x, [ I superscript negative sign ] subscript i minus x. The third column has the following: 0, positive x, [ I superscript negative sign ] subscript i plus x.

Since the equilibrium concentration of I2 is given, we can solve for x. At equilibrium the concentration of I2 is 6.61 × 10−4M so that

[latex]\begin{array}{rl @{{}={}} l} 1.000\;\times\;10^{-3}\;-\;x & = 6.61\;\times\;10^{-4} \\[0.5em] x & = 1.000\;\times\;10^{-3}\;-\;6.61\;\times\;10^{-4} \\[0.5em] x & = 3.39\;\times\;10^{-4}\;M \end{array}[/latex]

 

Now we can fill in the table with the concentrations at equilibrium.
This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following in the first column: Initial concentration ( M ), Change ( M ), Equilibrium concentration ( M ). The second column has the header, “I subscript 2 plus sign I superscript negative sign equilibrium arrow I subscript 3 superscript negative sign.” Under the second column is a subgroup of three rows and three columns. The first column has the following: 1.000 times 10 to the negative third power, negative x equals negative 3.39 times 10 to the negative fourth power, 6.61 times 10 to the negative fourth power. The second column has the following: 1.000 times 10 to the negative third power, negative x, 6.61 times 10 to the negative fourth power. The third column has the following: 0, positive x, 3.39 times 10 to the negative fourth power.

We now calculate the value of the equilibrium constant.

[latex]\begin{array}{rl @{{}={}} l} K_c & = \frac{[\text{I}_3^{\;\;-}]}{[\text{I}_2][\text{I}^{-}]} \\[1em] & = \frac{3.39\;\times\;10^{-4}\;M}{(6.61\;\times\;10^{-4}\;M)(6.61\;\times\;10^{-4}\;M)} \\[1em] & = 776 \end{array}[/latex]

 

Check Your Learning
Ethanol and acetic acid react and form water and ethyl acetate, the solvent responsible for the odor of some nail polish removers.

[latex]\text{C}_2\text{H}_5\text{OH}\;+\;\text{CH}_3\text{CO}_2\text{H}\;{\rightleftharpoons}\;\text{CH}_3\text{CO}_2\text{C}_2\text{H}_5\;+\;\text{H}_2\text{O}[/latex]

When 1 mol each of C2H5OH and CH3CO2H are allowed to react in 1 L of the solvent dioxane, equilibrium is established when 1313 mol of each of the reactants remains. Calculate the equilibrium constant for the reaction. (Note: Water is not a solvent in this reaction.)

Answer:

Kc = 4

Calculation of a Missing Equilibrium Concentration

If we know the equilibrium constant for a reaction and know the concentrations at equilibrium of all reactants and products except one, we can calculate the missing concentration.

Example 3

Calculation of a Missing Equilibrium Concentration
Nitrogen oxides are air pollutants produced by the reaction of nitrogen and oxygen at high temperatures. At 2000 °C, the value of the equilibrium constant for the reaction, [latex]\text{N}_2(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{NO}(g)[/latex], is 4.1 × 10−4. Find the concentration of NO(g) in an equilibrium mixture with air at 1 atm pressure at this temperature. In air, [N2] = 0.036 mol/L and [O2] 0.0089 mol/L.

Solution
We are given all of the equilibrium concentrations except that of NO. Thus, we can solve for the missing equilibrium concentration by rearranging the equation for the equilibrium constant.

[latex]\begin{array}{rl @{{}={}} l} K_c & = \frac{[\text{NO}]^2}{[\text{N}_2][\text{O}_2]}\\[0.5em] [\text{NO}]^2 & = K_c[\text{N}_2][\text{O}_2] \\[0.5em] [\text{NO}] & = \sqrt{K_c[\text{N}_2][\text{O}_2]}\\[0.5em] & = \sqrt{(4.1\;\times\;10^{-4})(0.036)(0.0089)}\\[0.5em] & = \sqrt{1.31\;\times\;10^{-7}}\\[0.5em] & = 3.6\;\times\;10^{-4} \end{array}[/latex]

 

Thus [NO] is 3.6 × 10−4 mol/L at equilibrium under these conditions.

We can check our answer by substituting all equilibrium concentrations into the expression for the reaction quotient to see whether it is equal to the equilibrium constant.

[latex]\begin{array}{rl @{{}={}} l} Q_c & = \frac{[\text{NO}]^2}{[\text{N}_2][\text{O}_2]} \\[1em] & = \frac{(3.6\;\times\;10^{-4})^2}{(0.036)(0.0089)}\\[1em] Q_c & = 4.0\;\times\;10^{-4} = K_c \end{array}[/latex]

 

The answer checks; our calculated value gives the equilibrium constant within the error associated with the significant figures in the problem.

Check Your Learning
The equilibrium constant for the reaction of nitrogen and hydrogen to produce ammonia at a certain temperature is 6.00 × 10−2. Calculate the equilibrium concentration of ammonia if the equilibrium concentrations of nitrogen and hydrogen are 4.26 M and 2.09 M, respectively.

Answer:

1.53 mol/L

Calculation of Changes in Concentration

If we know the equilibrium constant for a reaction and a set of concentrations of reactants and products that are not at equilibrium, we can calculate the changes in concentrations as the system comes to equilibrium, as well as the new concentrations at equilibrium. The typical procedure can be summarized in four steps.

  1. Determine the direction the reaction proceeds to come to equilibrium.
    1. Write a balanced chemical equation for the reaction.
    2. If the direction in which the reaction must proceed to reach equilibrium is not obvious, calculate Qc from the initial concentrations and compare to Kc to determine the direction of change.
  2. Determine the relative changes needed to reach equilibrium, then write the equilibrium concentrations in terms of these changes.
    1. Define the changes in the initial concentrations that are needed for the reaction to reach equilibrium. Generally, we represent the smallest change with the symbol x and express the other changes in terms of the smallest change.
    2. Define missing equilibrium concentrations in terms of the initial concentrations and the changes in concentration determined in (a).
  3. Solve for the change and the equilibrium concentrations.
    1. Substitute the equilibrium concentrations into the expression for the equilibrium constant, solve for x, and check any assumptions used to find x.
    2. Calculate the equilibrium concentrations.
  4. Check the arithmetic.
    1. Check the calculated equilibrium concentrations by substituting them into the equilibrium expression and determining whether they give the equilibrium constant.

      Sometimes a particular step may differ from problem to problem—it may be more complex in some problems and less complex in others. However, every calculation of equilibrium concentrations from a set of initial concentrations will involve these steps.

      In solving equilibrium problems that involve changes in concentration, sometimes it is convenient to set up an ICE table, as described in the previous section.

Example 4

Calculation of Concentration Changes as a Reaction Goes to Equilibrium
Under certain conditions, the equilibrium constant for the decomposition of PCl5(g) into PCl3(g) and Cl2(g) is 0.0211. What are the equilibrium concentrations of PCl5, PCl3, and Cl2 if the initial concentration of PCl5 was 1.00 M?

Solution
Use the stepwise process described earlier.

  1. Determine the direction the reaction proceeds.

    The balanced equation for the decomposition of PCl5 is

    [latex]\text{PCl}_5(g)\;{\rightleftharpoons}\;\text{PCl}_3(g)\;+\;\text{Cl}_2(g)[/latex]

    Because we have no products initially, Qc = 0 and the reaction will proceed to the right.

  2. Determine the relative changes needed to reach equilibrium, then write the equilibrium concentrations in terms of these changes.

    Let us represent the increase in concentration of PCl3 by the symbol x. The other changes may be written in terms of x by considering the coefficients in the chemical equation.

    [latex]\begin{array}{lcccc} \text{PCl}_5(g) & {\rightleftharpoons} & \text{PCl}_3(g) & + & \text{Cl}_2(g) \\[0.5em] -x & & x & & x \end{array}[/latex]

    The changes in concentration and the expressions for the equilibrium concentrations are:
    This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following in the first column: Initial concentration ( M ), Change ( M ), Equilibrium concentration ( M ). The second column has the header, “P C l subscript 5 equilibrium arrow P C l subscript 3 plus C l subscript 2.” Under the second column is a subgroup of three rows and three columns. The first column has the following: 1.00, negative x, 1.00 minus x. The second column has the following: 0, positive x, 0 plus x equals x. The third column has the following: 0, positive x, 0 plus x equals x.

  3. Solve for the change and the equilibrium concentrations.

    Substituting the equilibrium concentrations into the equilibrium constant equation gives

    [latex]\begin{array}{rl @{{}={}} l} K_c & = \frac{[\text{PCl}_3][\text{Cl}_2]}{[\text{PCl}_5]} & = 0.0211\\[0.5em] & = \frac{(x)(x)}{(1.00\;-\;x)} & = 0.0211\end{array}\\[0.5em][/latex]

    This equation contains only one variable, x, the change in concentration. We can write the equation as a quadratic equation and solve for x using the quadratic formula.

    [latex]\begin{array}{rl @{{}={}} l} 0.0211 & = \frac{(x)(x)}{(1.00\;-\;x)} \\[0.5em] 0.0211(1.00\;-\;x) & = x^2 \\[0.5em] x^2\;+\;0.0211x\;-\;0.0211 & = 0\end{array}\\[0.5em][/latex]

    Appendix B shows us an equation of the form ax2 + bx + c = 0 can be rearranged to solve for x:

    [latex]x = \frac{-b\;{\pm}\;\sqrt{b^2\;-\;4ac}}{2a}[/latex]

    In this case, a = 1, b = 0.0211, and c = −0.0211. Substituting the appropriate values for a, b, and c yields:

    [latex]\begin{array}{rl @{{}={}} l} x & = \frac{-0.0211\;{\pm}\;\sqrt{(0.0211)^2\;-\;4(1)(-0.0211)}}{2(1)}\\[0.5em] & = \frac{-0.0211\;{\pm}\;\sqrt{(4.45\;\times\;10^{-4})\;+\;(8.44\;\times\;10^{-2})}}{2} \\[0.5em] & = \frac{-0.0211\;{\pm}\;0.291}{2} \end{array}[/latex]

    Hence

    [latex]x = \frac{-0.0211\;+\;0.291}{2} = 0.135[/latex]

    or

    [latex]x = \frac{-0.0211\;-\;0.291}{2} = -0.156[/latex]

    Quadratic equations often have two different solutions, one that is physically possible and one that is physically impossible (an extraneous root). In this case, the second solution (−0.156) is physically impossible because we know the change must be a positive number (otherwise we would end up with negative values for concentrations of the products). Thus, x = 0.135 M.

    The equilibrium concentrations are

    [latex][\text{PCl}_5] = 1.00\;-\;0.135 = 0.87\;M\\[0.5em][/latex]
    [latex][\text{PCl}_3] = x = 0.135\;M\\[0.5em][/latex]
    [latex][\text{Cl}_2] = x = 0.135\;M\\[0.5em][/latex]
  4. Check the arithmetic.

    Substitution into the expression for Kc (to check the calculation) gives

    [latex]K_c = \frac{[\text{PCl}_3][\text{Cl}_2]}{[\text{PCl}_5]} = \frac{(0.135)(0.135)}{0.87} = 0.021[/latex]

    The equilibrium constant calculated from the equilibrium concentrations is equal to the value of Kc given in the problem (when rounded to the proper number of significant figures). Thus, the calculated equilibrium concentrations check.

Check Your Learning
Acetic acid, CH3CO2H, reacts with ethanol, C2H5OH, to form water and ethyl acetate, CH3CO2C2H5.

[latex]\text{CH}_3\text{CO}_2\text{H}\;+\;\text{C}_2\text{H}_5\text{OH}\;{\leftrightharpoons}\;\text{CH}_3\text{CO}_2\text{C}_2\text{H}_5\;+\;\text{H}_2\text{O}[/latex]

The equilibrium constant for this reaction with dioxane as a solvent is 4.0. What are the equilibrium concentrations when a mixture that is 0.15 M in CH3CO2H, 0.15 M in C2H5OH, 0.40 M in CH3CO2C2H5, and 0.40 M in H2O are mixed in enough dioxane to make 1.0 L of solution?

Answer:

[CH3CO2H] = 0.36 M, [C2H5OH] = 0.36 M, [CH3CO2C2H5] = 0.17 M, [H2O] = 0.17 M

Check Your Learning
A 1.00-L flask is filled with 1.00 moles of H2 and 2.00 moles of I2. The value of the equilibrium constant for the reaction of hydrogen and iodine reacting to form hydrogen iodide is 50.5 under the given conditions. What are the equilibrium concentrations of H2, I2, and HI in moles/L?

[latex]\text{H}_2(g)\;+\;\text{I}_2(g)\;{\leftrightharpoons}\;2\text{HI}(g)[/latex]

Answer:

[H2] = 0.06 M, [I2] = 1.06 M, [HI] = 1.88 M

Sometimes it is possible to use chemical insight to find solutions to equilibrium problems without actually solving a quadratic (or more complicated) equation. First, however, it is useful to verify that equilibrium can be obtained starting from two extremes: all (or mostly) reactants and all (or mostly) products (similar to what was shown in Figure 2 in Chapter 13.2 Equilibrium Constants).

Consider the ionization of 0.150 M HA, a weak acid.

[latex]\text{HA}(aq)\;{\rightleftharpoons}\;\text{H}^{+}(aq)\;+\;\text{A}^{-}(aq)\;\;\;\;\;\;\;K_c = 6.80\;\times\;10^{-4}[/latex]

The most obvious way to determine the equilibrium concentrations would be to start with only reactants. This could be called the “all reactant” starting point. Using x for the amount of acid ionized at equilibrium, this is the ICE table and solution.
This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following: Initial pressure ( M ), Change ( M ), Equilibrium ( M ). The second column has the header, “H A ( a q ) equilibrium arrow H superscript plus sign ( a q ) plus A subscript negative sign ( a q ).” Under the second column is a subgroup of three columns and three rows. The first column has the following: 0.150, negative x, 0.150 minus x. The second column has the following: 0, x, x. The third column has the following: 0, x, x.

Setting up and solving the quadratic equation gives

[latex]K_c = \frac{[\text{H}^{+}][\text{A}^{-}]}{[\text{HA}]} = \frac{(x)(x)}{(0.150\;-\;x)} = 6.80\;\times\;10^{-4}\\[1em][/latex]
[latex]x^2\;+\;(6.80\;\times\;10^{-4}x)\;-\;(1.02\;\times\;10^{-4}) = 0\\[1em][/latex]
[latex]x = \frac{-6.80\;\times\;10^{-4}\;{\pm}\;\sqrt{(6.80\;\times\;10^{-4})^2\;-\;(4)(1)(-1.02\;\times\;10^{-4})}}{(2)(1)}\\[1em][/latex]
[latex]x = 0.00977\;M\;\text{or}\;-0.0104\;M\\[0.5em][/latex]

Using the positive (physical) root, the equilibrium concentrations are

[latex][\text{HA}] = 0.150\;-\;x = 0.140\;M[/latex]
[latex][\text{H}^{+}] = [\text{A}^{-}] = x = 0.00977\;M[/latex]

A less obvious way to solve the problem would be to assume all the HA ionizes first, then the system comes to equilibrium. This could be called the “all product” starting point. Assuming all of the HA ionizes gives

[latex][\text{HA}] = 0.150\;-\;0.150 = 0\;M[/latex]
[latex][\text{H}^{+}] = 0\;+\;0.150 = 0.150\;M[/latex]
[latex][\text{A}^{-}] = 0\;+\;0.150 = 0.150\;M[/latex]

Using these as initial concentrations and “y” to represent the concentration of HA at equilibrium, this is the ICE table for this starting point.
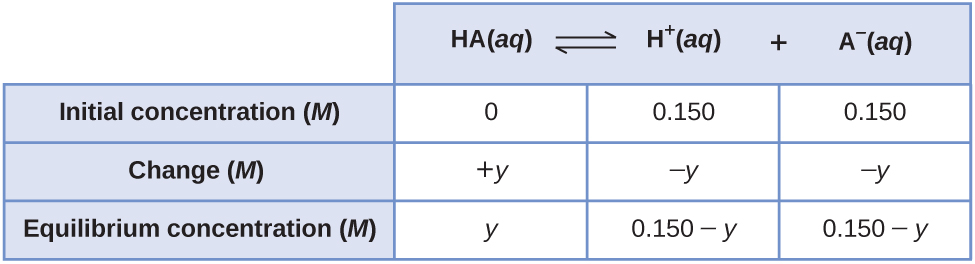
This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following: Initial pressure ( M ), Change ( M ), Equilibrium ( M ). The second column has the header, “H A ( a q ) equilibrium arrow H superscript plus sign ( a q ) plus A subscript negative sign ( a q ).” Under the second column is a subgroup of three columns and three rows. The first column has the following: 0, positive y, y. The second column has the following: 0.150, negative y, 0.150 minus y. The third column has the following: 0.150, negative y, and 0.150 minus y.

Setting up and solving the quadratic equation gives

[latex]K_c = \frac{[\text{H}^{+}][\text{A}^{-}]}{[\text{HA}]} = \frac{(0.150\;-\;y)(0.150\;-\;y)}{(y)} = 6.80\;\times\;10^{-4}\\[1em][/latex]
[latex]6.80\;\times\;10^{-4}y = 0.0225\;-\;0.300y\;+\;y^2\\[0.5em][/latex]

Retain a few extra significant figures to minimize rounding problems.

[latex]y^2\;-\;0.30068y\;+\;0.022500 = 0\\[1em][/latex]
[latex]y = \frac{0.30068\;{\pm}\;\sqrt{(0.30068)^2\;-\;(4)(1)(0.022500)}}{(2)(1)}\\[1em][/latex]
[latex]y = \frac{0.30068\;{\pm}\;0.020210}{2}\\[0.5em][/latex]

Rounding each solution to three significant figures gives

[latex]y = 0.160\;M\;\;\;\;\;\;\;\text{or}\;\;\;\;\;\;\;y = 0.140\;M[/latex]

Using the physically significant root (0.140 M) gives the equilibrium concentrations as

[latex][\text{HA}] = y = 0.140\;M[/latex]
[latex][\text{H}^{+}] = 0.150\;-\;y = 0.010\;M[/latex]
[latex][\text{A}^{-}] = 0.150\;-\;y = 0.010\;M[/latex]

Thus, the two approaches give the same results (to three decimal places), and show that both starting points lead to the same equilibrium conditions. The “all reactant” starting point resulted in a relatively small change (x) because the system was close to equilibrium, while the “all product” starting point had a relatively large change (y) that was nearly the size of the initial concentrations. It can be said that a system that starts “close” to equilibrium will require only a ”small” change in conditions (x) to reach equilibrium.

Recall that a small Kc means that very little of the reactants form products and a large Kc means that most of the reactants form products. If the system can be arranged so it starts “close” to equilibrium, then if the change (x) is small compared to any initial concentrations, it can be neglected. Small is usually defined as resulting in an error of less than 5%. The following two examples demonstrate this.

Example 5

Approximate Solution Starting Close to Equilibrium
What are the concentrations at equilibrium of a 0.15 M solution of HCN?

[latex]\text{HCN}(aq)\;{\rightleftharpoons}\;\text{H}^{+}(aq)\;+\;\text{CN}^{-}(aq)\;\;\;\;\;\;\;K_c = 4.9\;\times\;10^{-10}[/latex]

Solution
Using “x” to represent the concentration of each product at equilibrium gives this ICE table.
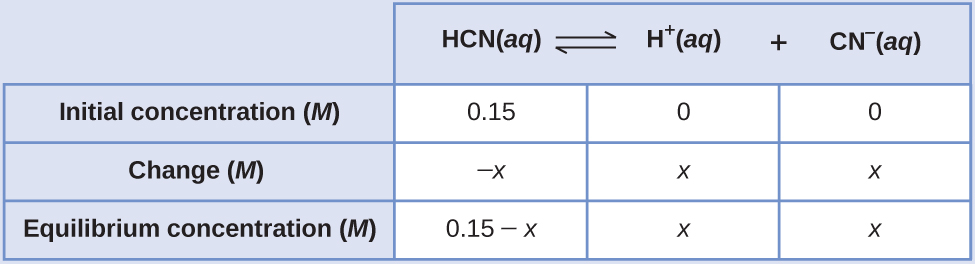
This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following: Initial pressure ( M ), Change ( M ), Equilibrium ( M ). The second column has the header, “H C N ( a q ) equilibrium arrow H superscript plus sign ( a q ) plus C N subscript negative sign ( a q ).” Under the second column is a subgroup of three columns and three rows. The first column has the following: 0.15, negative x, 0.15 minus x. The second column has the following: 0, x, x. The third column has the following: 0, x, x.

The exact solution may be obtained by solving for x in

[latex]K_c = 4.9\;\times\;10^{-10} = \frac{(x)(x)}{0.15\;-\;x}[/latex]

 

which, once multiplied through and rearranged, becomes

[latex]x^2\;+\;4.9\;\times\;10^{-10}\;-\;7.35\;\times\;10^{-11} = 0[/latex]

 

Using the quadratic formula with the above, x is determined to be

[latex]x = 8.5\underline{6}\;\times\;10^{-6}\;M\; = 8.6\;\times\;10^{-6}\;M\;[/latex]

 

Thus [H+] = [CN–] = x = 8.6 × 10–6M and [HCN] = 0.15 – x = 0.15 M.

In this case, chemical intuition can provide a simpler solution. From the equilibrium constant and the initial conditions, x must be small compared to 0.15 M. More formally, if [latex]x\;{\ll}\;0.15[/latex], then 0.15 – x ≈ 0.15. If this assumption is true, then it simplifies obtaining x

[latex]\begin{array}{rl @{{}={}} l} K_c & = \frac{(x)(x)}{0.15\;-\;x}\;{\approx}\;\frac{x^2}{0.15}\\[0.5em] 4.9\;\times\;10^{-10} & = \frac{x^2}{0.15} \\[0.5em] x^2 & = (0.15)(4.9\;\times\;10^{-10}) \\[0.5em] & = 7.4\;\times\;10^{-11} \\[0.5em] x & = \sqrt{7.4\;\times\;10^{-11}} \\[0.5em] & = 8.6\;\times\;10^{-6}\;M\end{array}[/latex]

 

In this example, solving the exact (quadratic) equation and using approximations gave the same result to two significant figures. While most of the time the approximation is a bit different from the exact solution, as long as the error is less than 5%, the approximate solution is considered valid. In this problem, the 5% applies to IF (0.15 – x) ≈ 0.15 M, so if

[latex]\frac{x}{0.15}\;\times\;100\% = \frac{8.6\;\times\;10^{-6}}{0.15}\;\times\;100\% = 0.006\%[/latex]

 

is less than 5%, as it is in this case, the assumption is valid. The approximate solution is thus a valid solution.

Check Your Learning
What are the equilibrium concentrations in a 0.25 M NH3 solution?

[latex]\text{NH}_3(aq)\;+\;\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{NH}_4^{\;\;+}(aq)\;+\;\text{OH}^{-}(aq)\;\;\;\;K_c = 1.8\;\times\;10^{-5}[/latex]

Assume that x is much less than 0.25 M and calculate the error in your assumption.

Answer:

[latex][\text{OH}^{-}] = [\text{NH}_4^{\;\;+}] = 0.0021\;M[/latex]; [NH3] = 0.25 M, error = 0.84%

The second example requires that the original information be processed a bit, but it still can be solved using a small x approximation.

Example 6

Approximate Solution After Shifting Starting Concentration
Copper(II) ions form a complex ion in the presence of ammonia

[latex]\text{Cu}^{2+}(aq)\;+\;4\text{NH}_3(aq)\;{\rightleftharpoons}\;\text{Cu(NH}_3)_4^{\;\;2+}(aq)\;\;\;\;\;\;\;\;\;\;\;K_c = 5.0\;\times\;10^{13} \\[0.5em][/latex]
[latex]K_c = \frac{[\text{Cu(NH}_3)_4^{\;\;2+}]}{[\text{Cu}^{2+}][\text{NH}_3]^4}[/latex]

 

If 0.010 mol Cu2+ is added to 1.00 L of a solution that is 1.00 M NH3 what are the concentrations when the system comes to equilibrium?

Solution
The initial concentration of copper(II) is 0.010 M. The equilibrium constant is very large so it would be better to start with as much product as possible because “all products” is much closer to equilibrium than “all reactants.” Note that Cu2+ is the limiting reactant; if all 0.010 M of it reacts to form product the concentrations would be

[latex][\text{Cu}^{2+}] = 0.010\;-\;0.010 = 0\;M[/latex]
[latex][\text{Cu(NH}_3)_4^{\;\;2+}] = 0.010\;M[/latex]
[latex][\text{NH}_3] = 1.00\;-\;4\;\times\;0.010 = 0.96\;M[/latex]

Using these “shifted” values as initial concentrations with x as the free copper(II) ion concentration at equilibrium gives this ICE table.
This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following: Initial pressure ( M ), Change ( M ), Equilibrium ( M ). The second column has the header, “C u superscript 2 positive sign ( a q ) plus 4 N H subscript 3 ( a q ) equilibrium arrow C u ( N H subscript 3 ) subscript 4 superscript 2 positive sign ( a q ).” Under the second column is a subgroup of three columns and three rows. The first column has the following: 0, positive x, x. The second column has the following: 0.96, positive 4 x, 0.96 plus 4 x. The third column has the following: 0.010, negative x, 0.010 minus x.

Since we are starting close to equilibrium, x should be small so that

[latex]\begin{array}{rl @{{}={}} l} 0.96\;+\;4x & {\approx}\;0.96\;M \\[0.5em] 0.010\;-\;x & {\approx}\;0.010\;M \end{array}[/latex]

 

Plugging this in:
[latex]K_c = \frac{(0.010\;-\;x)}{x(0.96\;-\;4x)^4}\; {\approx}\;\frac{(0.010)}{x(0.96)^4} = 5.0\;\times\;10^{13}[/latex]

 

and rearrange to solive for x:
[latex]x = \frac{(0.010)}{K_c(0.96)^4} = 2.4\;\times\;10^{-16}\;M[/latex]

 

Select the smallest concentration for the 5% rule.

[latex]\frac{2.4\;\times\;10^{-16}}{0.010}\;\times\;100\% = 2\;\times\;10^{-12}\%[/latex]

 

This is much less than 5%, so the assumptions are valid. The concentrations at equilibrium are

[latex][\text{Cu}^{2+}] = x = 2.4\;\times\;10^{-16}\;M[/latex]
[latex][\text{NH}_3] = 0.96\;-\;4x = 0.96\;M[/latex]
[latex][\text{Cu(NH}_3)_4^{\;\;2+}] = 0.010\;-\;x = 0.010\;M[/latex]

 

By starting with the maximum amount of product, this system was near equilibrium and the change (x) was very small. With only a small change required to get to equilibrium, the equation for x was greatly simplified and gave a valid result well within the 5% error maximum.

Check Your Learning
What are the equilibrium concentrations when 0.25 mol Ni2+ is added to 1.00 L of 2.00 M NH3 solution?

[latex]\text{Ni}^{2+}(aq)\;+\;6\text{NH}_3(aq)\;{\rightleftharpoons}\;\text{Ni(NH}_3)_6^{\;\;2+}(aq)\;\;\;\;\;\;\;K_c = 5.5\;\times\;10^8[/latex]

With such a large equilibrium constant, first form as much product as possible, then assume that only a small amount (x) of the product shifts left. Calculate the error in your assumption.

Answer:

[latex][\text{Ni(NH}_3)_6^{\;\;2+}] = 0.25\;M[/latex], [NH3] = 0.50 M, [Ni2+] = 2.9 × 10–8M, error = 1.2 × 10–5%

Key Concepts and Summary

The ratios of the rate of change in concentrations of a reaction are equal to the ratios of the coefficients in the balanced chemical equation. The sign of the coefficient of X is positive when the concentration increases and negative when it decreases. We learned to approach three basic types of equilibrium problems. When given the concentrations of the reactants and products at equilibrium, we can solve for the equilibrium constant; when given the equilibrium constant and some of the concentrations involved, we can solve for the missing concentrations; and when given the equilibrium constant and the initial concentrations, we can solve for the concentrations at equilibrium.

Chemistry End of Chapter Exercises

  1. A reaction is represented by this equation: [latex]\text{A}(aq)\;+\;2\text{B}(aq)\;{\rightleftharpoons}\;2\text{C}(aq)\;\;\;\;\;\;\;K_c = 1\;\times\;10^3[/latex]

    (a) Write the mathematical expression for the equilibrium constant.

    (b) Using concentrations ≤1 M, make up two sets of concentrations that describe a mixture of A, B, and C at equilibrium.

  2. A reaction is represented by this equation: [latex]2\text{W}(aq)\;{\rightleftharpoons}\;\text{X}(aq)\;+\;2\text{Y}(aq)\;\;\;\;\;\;\;K_c = 5\;\times\;10^{-4}[/latex]

    (a) Write the mathematical expression for the equilibrium constant.

    (b) Using concentrations of ≤1 M, make up two sets of concentrations that describe a mixture of W, X, and Y at equilibrium.

  3. What is the value of the equilibrium constant at 500 °C for the formation of NH3 according to the following equation?

    [latex]\text{N}_2(g)\;+\;3\text{H}_2(g)\;{\rightleftharpoons}\;2\text{NH}_3(g)[/latex]

    An equilibrium mixture of NH3(g), H2(g), and N2(g) at 500 °C was found to contain 1.35 M H2, 1.15 M N2, and 4.12 × 10−1M NH3.

  4. Hydrogen is prepared commercially by the reaction of methane and water vapor at elevated temperatures.

    [latex]\text{CH}_4(g)\;+\;\text{H}_2\text{O}(g)\;{\rightleftharpoons}\;3\text{H}_2(g)\;+\;\text{CO}(g)[/latex]

    What is the equilibrium constant for the reaction if a mixture at equilibrium contains gases with the following concentrations: CH4, 0.126 M; H2O, 0.242 M; CO, 0.126 M; H2 1.15 M, at a temperature of 760 °C?

  5. A 0.72-mol sample of PCl5 is put into a 1.00-L vessel and heated. At equilibrium, the vessel contains 0.40 mol of PCl3(g) and 0.40 mol of Cl2(g). Calculate the value of the equilibrium constant for the decomposition of PCl5 to PCl3 and Cl2 at this temperature.
  6. At 1 atm and 25 °C, NO2 with an initial concentration of 1.00 M is 3.3 × 10−3% decomposed into NO and O2. Calculate the value of the equilibrium constant for the reaction.

    [latex]2\text{NO}_2(g)\;{\rightleftharpoons}\;2\text{NO}(g)\;+\;\text{O}_2(g)[/latex]

  7. Calculate the value of the equilibrium constant KP for the reaction [latex]2\text{NO}(g)\;+\;\text{Cl}_2(g)\;{\rightleftharpoons}\;2\text{NOCl}(g)[/latex] from these equilibrium pressures: NO, 0.050 atm; Cl2, 0.30 atm; NOCl, 1.2 atm.
  8. When heated, iodine vapor dissociates according to this equation:

    [latex]\text{I}_2(g)\;{\rightleftharpoons}\;2\text{I}(g)[/latex]

    At 1274 K, a sample exhibits a partial pressure of I2 of 0.1122 atm and a partial pressure due to I atoms of 0.1378 atm. Determine the value of the equilibrium constant, KP, for the decomposition at 1274 K.

  9. A sample of ammonium chloride was heated in a closed container.

    [latex]\text{NH}_4\text{Cl}(s)\;{\rightleftharpoons}\;\text{NH}_3(g)\;+\;\text{HCl}(g)[/latex]

    At equilibrium, the pressure of NH3(g) was found to be 1.75 atm. What is the value of the equilibrium constant KP for the decomposition at this temperature?

  10. At a temperature of 60 °C, the vapor pressure of water is 0.196 atm. What is the value of the equilibrium constant KP for the transformation at 60 °C?

    [latex]\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{H}_2\text{O}(g)[/latex]

  11. Complete the changes in concentrations (or pressure, if requested) for each of the following reactions.

    (a)

    [latex]\begin{array}{lcccc} 2\text{SO}_3(g) & {\rightleftharpoons} & 2\text{SO}_2(g) & + & \text{O}_2(g) \\[0.5em] \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} & & +x \\[0.5em] \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} & & 0.125\;M \end{array}[/latex]

    (b)

    [latex]\begin{array}{lcccccc} 4\text{NH}_3(g) & + & 3\text{O}_2(g) & {\rightleftharpoons} & 2\text{N}_2(g) & + & 6\text{H}_2\text{O}(g) \\[0.5em] \rule[0ex]{2.5em}{0.1ex} & & 3x & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} \\[0.5em] \rule[0ex]{2.5em}{0.1ex} & & 0.24\;M & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} \end{array}[/latex]

    (c) Change in pressure:

    [latex]\begin{array}{lcccc} 2\text{CH}_4(g) & {\rightleftharpoons} & \text{C}_2\text{H}_2(g) & + & 3\text{H}_2(g) \\[0.5em] \rule[0ex]{2.5em}{0.1ex} & & x & & \rule[0ex]{2.5em}{0.1ex} \\[0.5em] \rule[0ex]{2.5em}{0.1ex} & & 25\;\text{torr} & & \rule[0ex]{2.5em}{0.1ex} \end{array}[/latex]

    (d) Change in pressure:

    [latex]\begin{array}{lcccccc} \text{CH}_4(g) & + & \text{H}_2\text{O}(g) & {\rightleftharpoons} & \text{CO}(g) & + & 3\text{H}_2(g) \\[0.5em] \rule[0ex]{2.5em}{0.1ex} & & x & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} \\[0.5em] \rule[0ex]{2.5em}{0.1ex} & & 5\;\text{atm} & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} \end{array}[/latex]

    (e)

    [latex]\begin{array}{lcccc} \text{NH}_4\text{Cl}(s) & {\rightleftharpoons} & \text{NH}_3(g) & + & \text{HCl}(g) \\[0.5em] & & x & & \rule[0ex]{2.5em}{0.1ex} \\[0.5em] & & 1.03\;\times\;10^{-4}\;M & & \rule[0ex]{2.5em}{0.1ex} \end{array}[/latex]

    (f) change in pressure:

    [latex]\begin{array}{lcccc} \text{Ni}(s) & + & 4\text{CO}(g) & {\leftrightharpoons} & \text{Ni(CO)}_4(g) \\[0.5em] & & 4x & & \rule[0ex]{2.5em}{0.1ex} \\[0.5em] & & 0.40\;\text{atm} & & \rule[0ex]{2.5em}{0.1ex} \end{array}[/latex]

  12. Complete the changes in concentrations (or pressure, if requested) for each of the following reactions.

    (a)

    [latex]\begin{array}{lcccc} 2\text{H}_2(g) & + & \text{O}_2(g) & {\rightleftharpoons} & 2\text{H}_2\text{O}(g) \\[0.5em] \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} & &+2x \\[0.5em] \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} & & 1.50\;M \end{array}[/latex]

    (b)

    [latex]\begin{array}{lcccccc} \text{CS}_2(g) & + & 4\text{H}_2(g) & {\rightleftharpoons} & \text{CH}_4(g) & + & 2\text{H}_2\text{S}(g) \\[0.5em] x & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} \\[0.5em] 0.020\;M & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} \end{array}[/latex]

    (c) Change in pressure:

    [latex]\begin{array}{lcccc} \text{H}_2(g) & + & \text{Cl}_2(g) & {\rightleftharpoons} & 2\text{HCl}(g) \\[0.5em] x & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} \\[0.5em] 1.50\;\text{atm} & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} \end{array}[/latex]

    (d) Change in pressure:

    [latex]\begin{array}{lcccccc} 2\text{NH}_3(g) & + & 2\text{O}_2(g) & {\rightleftharpoons} & \text{N}_2\text{O}(g) & + & 3\text{H}_2\text{O}(g) \\[0.5em] \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} & & x \\[0.5em] \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} & & \rule[0ex]{2.5em}{0.1ex} & & 60.6\;\text{torr} \end{array}[/latex]

    (e)

    [latex]\begin{array}{lcccc} \text{NH}_4\text{HS}(s) & {\leftrightharpoons} & \text{NH}_3(g) & + & \text{H}_2\text{S}(g) \\[0.5em] & & x & & \rule[0ex]{2.5em}{0.1ex} \\[0.5em] & & 9.8\;\times\;10^{-6}\;M & & \rule[0ex]{2.5em}{0.1ex} \end{array}[/latex]

    (f) Change in pressure:

    [latex]\begin{array}{lcccc} \text{Fe}(s) & + & 5\text{CO}(g) & {\leftrightharpoons} & \text{Fe(CO)}_4(g) \\[0.5em] & & \rule[0ex]{2.5em}{0.1ex} & & x \\[0.5em] & & \rule[0ex]{2.5em}{0.1ex} & & 0.012\;\text{atm} \end{array}[/latex]

  13. Why are there no changes specified for Ni in Exercise 11, part (f)? What property of Ni does change?
  14. Why are there no changes specified for NH4HS in Exercise 12, part (e)? What property of NH4HS does change?
  15. Analysis of the gases in a sealed reaction vessel containing NH3, N2, and H2 at equilibrium at 400 °C established the concentration of N2 to be 1.2 M and the concentration of H2 to be 0.24 M.

    [latex]\text{N}_2(g)\;+\;3\text{H}_2(g)\;{\rightleftharpoons}\;2\text{NH}_3(g)\;\;\;\;\;\;\;K_c = 0.50\;\text{at}\;400\;^{\circ}\text{C}[/latex]

    Calculate the equilibrium molar concentration of NH3.

  16. Calculate the number of moles of HI that are at equilibrium with 1.25 mol of H2 and 1.25 mol of I2 in a 5.00−L flask at 448 °C.

    [latex]\text{H}_2\;+\;\text{I}_2\;{\rightleftharpoons}\;2\text{HI}\;\;\;\;\;\;\;K_c = 50.2\;\text{at}\;448\;^{\circ}\text{C}[/latex]

  17. What is the pressure of BrCl in an equilibrium mixture of Cl2, Br2, and BrCl if the pressure of Cl2 in the mixture is 0.115 atm and the pressure of Br2 in the mixture is 0.450 atm?

    [latex]\text{Cl}_2(g)\;+\;\text{Br}_2(g)\;{\rightleftharpoons}\;2\text{BrCl}(g)\;\;\;\;\;\;\;K_P = 4.7\;\times\;10^{-2}[/latex]

  18. What is the pressure of CO2 in a mixture at equilibrium that contains 0.50 atm H2, 2.0 atm of H2O, and 1.0 atm of CO at 990 °C?

    [latex]\text{H}_2(g)\;+\;\text{CO}_2(g)\;{\rightleftharpoons}\;\text{H}_2\text{O}(g)\;+\;\text{CO}(g)\;\;\;\;\;\;\;K_P = 1.6\;\text{at}\;990\;^{\circ}\text{C}[/latex]

  19. Cobalt metal can be prepared by reducing cobalt(II) oxide with carbon monoxide.

    [latex]\text{CoO}(s)\;+\;\text{CO}(g)\;{\rightleftharpoons}\;\text{Co}(s)\;+\;\text{CO}_2(g)\;\;\;\;\;\;\;K_c = 4.90\;\times\;10^2\;\text{at}\;550\;^{\circ}\text{C}[/latex]

    What concentration of CO remains in an equilibrium mixture with [CO2] = 0.100 M?

  20. Carbon reacts with water vapor at elevated temperatures.

    [latex]\text{C}(s)\;+\;\text{H}_2\text{O}(g)\;{\rightleftharpoons}\;\text{CO}(g)\;+\;\text{H}_2(g)\;\;\;\;\;\;\;K_c = 0.2\;\text{at}\;1000\;^{\circ}\text{C}[/latex]

    What is the concentration of CO in an equilibrium mixture with [H2O] = 0.500 M at 1000 °C?

  21. Sodium sulfate 10−hydrate, Na2SO4·10H2O, dehydrates according to the equation

    [latex]\text{Na}_2\text{SO}_4{\cdot}10\text{H}_2\text{O}(s)\;{\rightleftharpoons}\;\text{Na}_2\text{SO}_4(s)\;+\;10\text{H}_2\text{O}(g)\;\;\;\;\;\;\;K_P = 4.08\;\times\;10^{-25}\;\text{at}\;25\;^{\circ}\text{C}[/latex]

    What is the pressure of water vapor at equilibrium with a mixture of Na2SO4·10H2O and NaSO4?

  22. Calcium chloride 6−hydrate, CaCl2·6H2O, dehydrates according to the equation

    [latex]\text{CaCl}_2{\cdot}6\text{H}_2\text{O}(s)\;{\rightleftharpoons}\;\text{CaCl}_2(s)\;+\;6\text{H}_2\text{O}(g)\;\;\;\;\;\;\;K_P = 5.09\;\times\;10^{-44}\;\text{at}\;25\;^{\circ}\text{C}[/latex]

    What is the pressure of water vapor at equilibrium with a mixture of CaCl2·6H2O and CaCl2?

  23. A student solved the following problem and found the equilibrium concentrations to be [SO2] = 0.590 M, [O2] = 0.0450 M, and [SO3] = 0.260 M. How could this student check the work without reworking the problem? The problem was: For the following reaction at 600 °C:

    [latex]2\text{SO}_2(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{SO}_3(g)\;\;\;\;\;\;\;K_c = 4.32[/latex]

    What are the equilibrium concentrations of all species in a mixture that was prepared with [SO3] = 0.500 M, [SO2] = 0 M, and [O2] = 0.350 M?

  24. A student solved the following problem and found [N2O4] = 0.16 M at equilibrium. How could this student recognize that the answer was wrong without reworking the problem? The problem was: What is the equilibrium concentration of N2O4 in a mixture formed from a sample of NO2 with a concentration of 0.10 M?

    [latex]2\text{NO}_2(g)\;{\rightleftharpoons}\;\text{N}_2\text{O}_4(g)\;\;\;\;\;\;\;K_c = 160[/latex]

  25. Assume that the change in concentration of N2O4 is small enough to be neglected in the following problem.
    (a) Calculate the equilibrium concentration of both species in 1.00 L of a solution prepared from 0.129 mol of N2O4 with chloroform as the solvent.

    [latex]\text{N}_2\text{O}_4(g)\;{\leftrightharpoons}\;2\text{NO}_2(g)\;\;\;\;\;\;\;K_c = 1.07\;\times\;10^{-5}[/latex] in chloroform

    (b) Show that the change is small enough to be neglected.

  26. Assume that the change in concentration of COCl2 is small enough to be neglected in the following problem.

    (a) Calculate the equilibrium concentration of all species in an equilibrium mixture that results from the decomposition of COCl2 with an initial concentration of 0.3166 M.

    [latex]\text{COCl}_2(g)\;{\rightleftharpoons}\;\text{CO}(g)\;+\;\text{Cl}_2(g)\;\;\;\;\;\;\;K_c = 2.2\;\times\;10^{-10}[/latex]

    (b) Show that the change is small enough to be neglected.

  27. Assume that the change in pressure of H2S is small enough to be neglected in the following problem.

    (a) Calculate the equilibrium pressures of all species in an equilibrium mixture that results from the decomposition of H2S with an initial pressure of 0.824 atm.

    [latex]2\text{H}_2\text{S}(g)\;{\rightleftharpoons}\;2\text{H}_2(g)\;+\;\text{S}_2(g)\;\;\;\;\;\;\;K_P = 2.2\;\times\;10^{-6}[/latex]

    (b) Show that the change is small enough to be neglected.

  28. What are all concentrations after a mixture that contains [H2O] = 1.00 M and [Cl2O] = 1.00 M comes to equilibrium at 25 °C?

    [latex]\text{H}_2\text{O}(g)\;+\;\text{Cl}_2\text{O}(g)\;{\rightleftharpoons}\;2\text{HOCl}(g)\;\;\;\;\;\;\;K_c = 0.0900[/latex]

  29. What are the concentrations of PCl5, PCl3, and Cl2 in an equilibrium mixture produced by the decomposition of a sample of pure PCl5 with [PCl5] = 2.00 M?

    [latex]\text{PCl}_5(g)\;{\rightleftharpoons}\;\text{PCl}_3(g)\;+\;\text{Cl}_2(g)\;\;\;\;\;\;\;K_c = 0.0211[/latex]

  30. Calculate the pressures of all species at equilibrium in a mixture of NOCl, NO, and Cl2 produced when a sample of NOCl with a pressure of 10.0 atm comes to equilibrium according to this reaction:
    [latex]2\text{NOCl}(g)\;{\rightleftharpoons}\;2\text{NO}(g)\;+\;\text{Cl}_2(g)\;\;\;\;\;\;\;K_P = 4.0\;\times\;10^{-4}[/latex]
  31. Calculate the equilibrium concentrations of NO, O2, and NO2 in a mixture at 250 °C that results from the reaction of 0.20 M NO and 0.10 M O2. (Hint: K is large; assume the reaction goes to completion then comes back to equilibrium.)

    [latex]2\text{NO}(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{NO}_2(g)\;\;\;\;\;\;\;K_c = 2.3\;\times\;10^5\;\text{at}\;250\;^{\circ}\text{C}[/latex]

  32. Calculate the equilibrium concentrations that result when 0.25 M O2 and 1.0 M HCl react and come to equilibrium.

    [latex]4\text{HCl}(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{Cl}_2(g)\;+\;2\text{H}_2\text{O}(g)\;\;\;\;\;\;\;K_c = 3.1\;\times\;10^{13}[/latex]

  33. One of the important reactions in the formation of smog is represented by the equation

    [latex]\text{O}_3(g)\;+\;\text{NO}(g)\;{\rightleftharpoons}\;\text{NO}_2(g)\;+\;\text{O}_2(g)\;\;\;\;\;\;\;K_P = 6.0\;\times\;10^{34}[/latex]

    What is the pressure of O3 remaining after a mixture of O3 with a pressure of 1.2 × 10−8 atm and NO with a pressure of 1.2 × 10−8 atm comes to equilibrium? (Hint: KP is large; assume the reaction goes to completion then comes back to equilibrium.)

  34. Calculate the pressures of NO, Cl2, and NOCl in an equilibrium mixture produced by the reaction of a starting mixture with 4.0 atm NO and 2.0 atm Cl2. (Hint: KP is small; assume the reverse reaction goes to completion then comes back to equilibrium.)

    [latex]2\text{NO}(g)\;+\;\text{Cl}_2(g)\;{\rightleftharpoons}\;2\text{NOCl}(g)\;\;\;\;\;\;\;K_P = 2.5\;\times\;10^3[/latex]

  35. Calculate the number of grams of HI that are at equilibrium with 1.25 mol of H2 and 63.5 g of iodine at 448 °C.

    [latex]\text{H}_2\;+\;\text{I}_2\;{\rightleftharpoons}\;2\text{HI}\;\;\;\;\;\;\;K_c = 50.2\;\text{at}\;448\;^{\circ}\text{C}[/latex]

  36. Butane exists as two isomers, n−butane and isobutane.
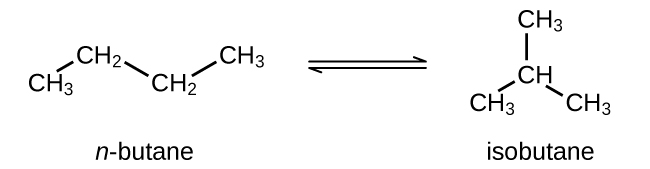
    Three Lewis structures are shown. The first is labeled, “n dash Butane,” and has a C H subscript 3 single bonded to a C H subscript 2 group. This C H subscript 2 group is single bonded to another C H subscript 2 group which is single bonded to a C H subscript 3 group. The second is labeled, “iso dash Butane,” and is composed of a C H group single bonded to three C H subscript 3 groups. The third structure shows a chain of atoms: “C H subscript 3, C H subscript 2, C H subscript 2, C H subscript 3,” a double-headed arrow, then a carbon atom single bonded to three C H subscript 3 groups as well as a hydrogen atom.

    KP = 2.5 at 25 °C

    What is the pressure of isobutane in a container of the two isomers at equilibrium with a total pressure of 1.22 atm?

  37. What is the minimum mass of CaCO3 required to establish equilibrium at a certain temperature in a 6.50-L container if the equilibrium constant (Kc) is 0.050 for the decomposition reaction of CaCO3 at that temperature?

    [latex]\text{CaCO}_3(s)\;{\rightleftharpoons}\;\text{CaO}(s)\;+\;\text{CO}_2(g)[/latex]

  38. The equilibrium constant (Kc) for this reaction is 1.60 at 990 °C:

    [latex]\text{H}_2(g)\;+\;\text{CO}_2(g)\;{\rightleftharpoons}\;\text{H}_2\text{O}(g)\;+\;\text{CO}(g)[/latex]

    Calculate the number of moles of each component in the final equilibrium mixture obtained from adding 1.00 mol of H2, 2.00 mol of CO2, 0.750 mol of H2O, and 1.00 mol of CO to a 5.00-L container at 990 °C.

  39. At 25 °C and at 1 atm, the partial pressures in an equilibrium mixture of N2O4 and NO2 are [latex]\text{P}_{\text{N}_2\text{O}_4} = 0.70\;\text{atm}[/latex] and [latex]\text{P}_{\text{NO}_2} = 0.30\;\text{atm}[/latex].

    (a) Predict how the pressures of NO2 and N2O4 will change if the total pressure increases to 9.0 atm. Will they increase, decrease, or remain the same?

    (b) Calculate the partial pressures of NO2 and N2O4 when they are at equilibrium at 9.0 atm and 25 °C.

  40. In a 3.0-L vessel, the following equilibrium partial pressures are measured: N2, 190 torr; H2, 317 torr; NH3, 1.00 × 103 torr.

    [latex]\text{N}_2(g)\;+\;3\text{H}_2(g)\;{\rightleftharpoons}\;2\text{NH}_3(g)[/latex]

    (a) How will the partial pressures of H2, N2, and NH3 change if H2 is removed from the system? Will they increase, decrease, or remain the same?

    (b) Hydrogen is removed from the vessel until the partial pressure of nitrogen, at equilibrium, is 250 torr. Calculate the partial pressures of the other substances under the new conditions.

  41. The equilibrium constant (Kc) for this reaction is 5.0 at a given temperature.

    [latex]\text{CO}(g)\;+\;\text{H}_2\text{O}(g)\;{\rightleftharpoons}\;\text{CO}_2(g)\;+\;\text{H}_2(g)[/latex]

    (a) On analysis, an equilibrium mixture of the substances present at the given temperature was found to contain 0.20 mol of CO, 0.30 mol of water vapor, and 0.90 mol of H2 in a liter. How many moles of CO2 were there in the equilibrium mixture?

    (b) Maintaining the same temperature, additional H2 was added to the system, and some water vapor was removed by drying. A new equilibrium mixture was thereby established containing 0.40 mol of CO, 0.30 mol of water vapor, and 1.2 mol of H2 in a liter. How many moles of CO2 were in the new equilibrium mixture? Compare this with the quantity in part (a), and discuss whether the second value is reasonable. Explain how it is possible for the water vapor concentration to be the same in the two equilibrium solutions even though some vapor was removed before the second equilibrium was established.

  42. Antimony pentachloride decomposes according to this equation:

    [latex]\text{SbCl}_5(g)\;{\rightleftharpoons}\;\text{SbCl}_3(g)\;+\;\text{Cl}_2(g)[/latex]

    An equilibrium mixture in a 5.00-L flask at 448 °C contains 3.85 g of SbCl5, 9.14 g of SbCl3, and 2.84 g of Cl2. How many grams of each will be found if the mixture is transferred into a 2.00-L flask at the same temperature?

  43. Consider the reaction between H2 and O2 at 1000 K
    [latex]2\text{H}_2(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{H}_2\text{O}(g)\;\;\;\;\;\;\;K_P = \frac{(P_{\text{H}_2\text{O}})^2}{(P_{\text{O}_2})(P_{\text{H}_2})^3} = 1.33\;\times\;10^{20}[/latex]

    If 0.500 atm of H2 and 0.500 atm of O2 are allowed to come to equilibrium at this temperature, what are the partial pressures of the components?

  44. An equilibrium is established according to the following equation

    [latex]\text{Hg}_2^{\;\;2+}(aq)\;+\;\text{NO}_3^{\;\;-}(aq)\;+\;3\text{H}^{+}(aq)\;{\rightleftharpoons}\;2\text{Hg}^{2+}(aq)\;+\;\text{HNO}_2(aq)\;+\;\text{H}_2\text{O}(l)\;\;\;\;\;\;\;K_c = 4.6[/latex]

    What will happen in a solution that is 0.20 M each in [latex]\text{Hg}_2^{\;\;2+}[/latex], [latex]\text{NO}_3^{\;\;-}[/latex], H+, Hg2+, and HNO2?

    (a) [latex]\text{Hg}_2^{\;\;2+}[/latex] will be oxidized and [latex]\text{NO}_3^{\;\;-}[/latex] reduced.

    (b) [latex]\text{Hg}_2^{\;\;2+}[/latex] will be reduced and [latex]\text{NO}_3^{\;\;-}[/latex] oxidized.

    (c) Hg2+ will be oxidized and HNO2 reduced.

    (d) Hg2+ will be reduced and HNO2 oxidized.

    (e) There will be no change because all reactants and products have an activity of 1.

  45. Consider the equilibrium

    [latex]4\text{NO}_2(g)\;+\;6\text{H}_2\text{O}(g)\;{\rightleftharpoons}\;4\text{NH}_3(g)\;+\;7\text{O}_2(g)[/latex]

    (a) What is the expression for the equilibrium constant (Kc) of the reaction?

    (b) How must the concentration of NH3 change to reach equilibrium if the reaction quotient is less than the equilibrium constant?

    (c) If the reaction were at equilibrium, how would a decrease in pressure (from an increase in the volume of the reaction vessel) affect the pressure of NO2?

    (d) If the change in the pressure of NO2 is 28 torr as a mixture of the four gases reaches equilibrium, how much will the pressure of O2 change?

  46. The binding of oxygen by hemoglobin (Hb), giving oxyhemoglobin (HbO2), is partially regulated by the concentration of H3O+ and dissolved CO2 in the blood. Although the equilibrium is complicated, it can be summarized as

    [latex]\text{HbO}_2(aq)\;+\;\text{H}_3\text{O}^{+}(aq)\;+\;\text{CO}_2(g)\;{\rightleftharpoons}\;\text{CO}_2\;-\;\text{Hb}\;-\;\text{H}^{+}\;+\;\text{O}_2(g)\;+\;\text{H}_2\text{O}(l)[/latex]

    (a) Write the equilibrium constant expression for this reaction.

    (b) Explain why the production of lactic acid and CO2 in a muscle during exertion stimulates release of O2 from the oxyhemoglobin in the blood passing through the muscle.

  47. The hydrolysis of the sugar sucrose to the sugars glucose and fructose follows a first-order rate equation for the disappearance of sucrose.

    [latex]\text{C}_{12}\text{H}_{22}\text{O}_{11}(aq)\;+\;\text{H}_2\text{O}(l)\;{\longrightarrow}\;\text{C}_6\text{H}_{12}\text{O}_6(aq)\;+\;\text{C}_6\text{H}_{12}\text{O}_6(aq)[/latex]

    Rate = k[C12H22O11]

    In neutral solution, k = 2.1 × 10−11/s at 27 °C. (As indicated by the rate constant, this is a very slow reaction. In the human body, the rate of this reaction is sped up by a type of catalyst called an enzyme.) (Note: That is not a mistake in the equation—the products of the reaction, glucose and fructose, have the same molecular formulas, C6H12O6, but differ in the arrangement of the atoms in their molecules). The equilibrium constant for the reaction is 1.36 × 105 at 27 °C. What are the concentrations of glucose, fructose, and sucrose after a 0.150 M aqueous solution of sucrose has reached equilibrium? Remember that the activity of a solvent (the effective concentration) is 1.

  48. The density of trifluoroacetic acid vapor was determined at 118.1 °C and 468.5 torr, and found to be 2.784 g/L. Calculate Kc for the association of the acid.
    Two Lewis structures are shown in a reaction. The first structure, which is condensed, reads, “2 C F subscript 3 C O subscript 2 H ( g ),” and is followed by a double-headed arrow. The second structure shows a partially condensed hexagonal ring shape. From the left side, in a clockwise manner, it reads “C F subscript 3 C, single bond, O, single bond, H, dotted line bond, O, double bond, C F subscript 3 C ( g ), single bond, O, single bond, H, dotted line bond, O, double bond back to the starting compound.”
  49. Liquid N2O3 is dark blue at low temperatures, but the color fades and becomes greenish at higher temperatures as the compound decomposes to NO and NO2. At 25 °C, a value of KP = 1.91 has been established for this decomposition. If 0.236 moles of N2O3 are placed in a 1.52-L vessel at 25 °C, calculate the equilibrium partial pressures of N2O3(g), NO2(g), and NO(g).
  50. A 1.00-L vessel at 400 °C contains the following equilibrium concentrations: N2, 1.00 M; H2, 0.50 M; and NH3, 0.25 M. How many moles of hydrogen must be removed from the vessel to increase the concentration of nitrogen to 1.1 M?
  51. A 0.010 M solution of the weak acid HA has an osmotic pressure (see chapter on solutions and colloids) of 0.293 atm at 25 °C. A 0.010 M solution of the weak acid HB has an osmotic pressure of 0.345 atm under the same conditions.

    (a) Which acid has the larger equilibrium constant for ionization – HA [latex][\text{HA}(aq)\;{\rightleftharpoons}\;\text{A}^{-}(aq)\;+\;\text{H}^{+}(aq)][/latex] or HB [latex][\text{HB}(aq)\;{\rightleftharpoons}\;\text{H}^{+}(aq)\;+\;\text{B}^{-}(aq)][/latex]?

    (b) What are the equilibrium constants for the ionization of these acids?

    (Hint: Remember that each solution contains three dissolved species: the weak acid (HA or HB), the conjugate base (A− or B−), and the hydrogen ion (H+). Remember that osmotic pressure (like all colligative properties) is related to the total number of solute particles. Specifically for osmotic pressure, those concentrations are described by molarities.)

Solutions

Answers to Chemistry End of Chapter Exercises

1. [latex]K_c = \frac{[\text{C}]^2}{[\text{A}][\text{B}]^2}[/latex]. [A] = 0.1 M, [B] = 0.1 M, [C] = 1 M; and [A] = 0.01, [B] = 0.250, [C] = 0.791.

3. Kc = 6.00 × 10−2

5. Kc = 0.50

7. The equilibrium equation is
KP = 1.9 × 103

9. KP = 3.06

11. (a) −2x, 2x, −0.250 M, 0.250 M; (b) 4x, −2x, −6x, 0.32 M, −0.16 M, −0.48 M; (c) −2x, 3x, −50 torr, 75 torr; (d) x, − x, −3x, 5 atm, −5 atm, −15 atm; (e) x, 1.03 × 10−4M; (f) x, 0.1 atm.

13. Activities of pure crystalline solids equal 1 and are constant; however, the mass of Ni does change.

15. [NH3] = 9.1 × 10−2M

17. PBrCl = 4.9 × 10−2 atm

19. [CO] = 2.0 × 10−4M

21. [latex]P_{\text{H}_2\text{O}} = 3.64\;\times\;10^{-3}\;\text{atm}[/latex]

23. Calculate Q based on the calculated concentrations and see if it is equal to Kc. Because Q does equal 4.32, the system must be at equilibrium.

25. (a) [NO2] = 1.17 × 10−3M
[N2O4] = 0.128 M
(b) Percent error [latex]= \frac{5.87\;\times\;10^{-4}}{0.129}\;\times\;100\% = 0.455\%[/latex]. The change in concentration of N2O4 is far less than the 5% maximum allowed.

27. (a) [H2S] = 0.810 atm
[H2] = 0.014 atm
[S2] = 0.0072 atm
(b) The 2x is dropped from the equilibrium calculation because 0.014 is negligible when subtracted from 0.824. The percent error associated with ignoring 2x is [latex]\frac{0.014}{0.824}\;\times\;100\% = 1.7\%[/latex], which is less than allowed by the “5% test.” The error is, indeed, negligible.

29. [PCl3] = 1.80 M; [PC3] = 0.195 M; [PCl3] = 0.195 M.

31. [NO2] = 0.19 M
[NO] = 0.0070 M
[O2] = 0.0035 M

33. [latex]P_{\text{O}_3} = 4.9\;\times\;10^{-26}\;\text{atm}[/latex]

35. 507 g

37. 330 g

39. (a) Both gases must increase in pressure.
(b)[latex]P_{\text{N}_2\text{O}_4} = 8.0\;\text{atm and}\;P_{\text{NO}_2} = 1.0\;\text{atm}[/latex]

41. (a) 0.33 mol.
(b) [CO]2 = 0.50 M Added H2 forms some water to compensate for the removal of water vapor and as a result of a shift to the left after H2 is added.

43. [latex]P_{\text{H}_2} = 8.64\;\times\;10^{-11}\;\text{atm}[/latex]
[latex]P_{\text{O}_2} = 0.250\;\text{atm}[/latex]
[latex]P_{\text{H}_2\text{O}} = 0.500\;\text{atm}[/latex]

45. (a) [latex]K_c = \frac{[\text{NH}_3]^4[\text{O}_2]^7}{[\text{NO}_2]^4[\text{H}_2\text{O}]^6}[/latex]. (b) [NH3] must increase for Qc to reach Kc. (c) That decrease in pressure would decrease [NO2]. (d) [latex]P_{\text{O}_2} = 49\;\text{torr}[/latex]

47. [fructose] = 0.15 M

49. [latex]P_{\text{N}_2\text{O}_3} = 1.90\;\text{atm and}\;P_{\text{NO}} = P_{\text{NO}_2} = 1.90\;\text{atm}[/latex]

51. (a) HB ionizes to a greater degree and has the larger Kc.
(b) Kc(HA) = 5 × 10−4    Kc(HB) = 3 × 10−3

License

Icon for the Creative Commons Attribution 4.0 International License

College of Western Idaho General Chemistry: CHEM 111 & 112 Copyright © 2016 by Rice University is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book