3

Deductive logic I: Aristotelian Logic

I. Deductive Logic

In this and the next 3 chapters we will study deductive logic and two approaches to evaluating deductive arguments. The first, which is the subject of the present chapter, was developed by Aristotle nearly 2,500 years ago, and we’ll refer to it simply as Aristotelian Logic; the second, the subject of the next chapter, has roots nearly as ancient as Aristotle’s but wasn’t fully developed until the 19^th century, and is called Propositional Logic.

Again, these are two different approaches to the same problem: evaluating deductive arguments, determining whether they are valid or invalid. Recall, deductive arguments are valid just in case their premises guarantee their conclusions; and validity is determined entirely by the form of the argument. The two logics we study will have different ways of identifying the logical form of arguments, and different methods of testing those forms for validity. These are two of the things a deductive logic must do: specify precise criteria for determining logical form and develop a way of testing it for validity.

But before a logic can do those two things, there is a preliminary job: it must tame natural language. Real arguments that we care about evaluating are expressed in natural languages like English, Greek, etc. As we saw in our discussion of the logical fallacies in the last chapter, natural languages are unruly: they are filled with ambiguity and vagueness, and exhibit an overall lack of precision that makes it very difficult to conduct the kind of rigorous analysis necessary to determine whether or not an argument is valid. So before making that determination, a logic must do some tidying up; it must remove the imprecision inherent in natural language expressions of arguments and make them suitable for rigorous analysis. There are various approaches to this task. Aristotelian Logic and Sentential logic adopt two different strategies.

Aristotelian Logic seeks to tame natural language by restricting itself to a well-behaved, precise portion of the language. It only evaluates arguments that are expressed within that precisely delimited subset of the language. Propositional logic achieves precision by eschewing natural language entirely: it constructs its own artificial language, and only evaluates arguments expressed in its terms.

This strategy may seem overly restrictive: if we limit ourselves to arguments expressed in a limited vocabulary—and especially if we leave behind natural language entirely—aren’t we going to miss lots of (all?) arguments that we care about? The answer is no, these approaches are not nearly as restrictive as they might seem. We can translate back and forth between the special portion of language in Aristotelian Logic and expressions in natural language that are outside its scope. Likewise, we can translate back and forth between the artificial language of Sentential logic and natural language. The process of translating from the unruly bits of natural language into these more precise alternatives is what removes the ambiguity, vagueness, etc. that stands in the way of rigorous analysis and evaluation. So, part of the task of taming natural language is showing how one’s alternative to it is nevertheless related to it—how it picks out the logically important features of natural language arguments while leaving behind their extraneous, recalcitrant bits.

These, then, are the three tasks that a deductive logic must accomplish:

1. Tame natural language.
2. Precisely define logical form.
3. Develop a way to test logical forms for validity.

The process for evaluating real arguments expressed in natural language is to render them precise and suitable for evaluation by translating them into the preferred vocabulary developed in step 1, then to identify and evaluate their forms according to the prescriptions of steps 2 and 3.

We now proceed to discuss Aristotelian Logic, starting with its approach to taming natural language.

II. Classes and Categorical Propositions

For Aristotle, the fundamental logical unit is the class. Classes are just sets of things—sets that we can pick out using language. The simplest way to identify a class is by using a plural noun: trees, clouds, asteroids, people—these are all classes. Names for classes can be grammatically more complex, too. We can modify the plural noun with an adjective: ‘rich people’ picks out a class. Prepositional phrases can further specify: ‘rich people from Italy’ picks out a different class. The modifications can go on indefinitely: ‘rich people from Italy who made their fortunes in real estate and whose grandmothers were rumored to be secret lovers of Benito Mussolini’ picks out yet another class—which is either very small, or possibly empty, I don’t know. (Empty classes are just classes with no members; we’ll talk more about them later.)

We will refer to names of classes as ‘class-terms’, or just ‘terms’ for short. Since for Aristotle the fundamental logical unit is the class, and since terms are the bits of language that pick out classes, Aristotle’s logic is often referred to as a ‘term logic’. This is in contrast to the method of logic we will study in the next chapter, Propositional Logic, so-called because it takes the fundamental logical unit to be the proposition.

Of course, Aristotelian Logic must also deal with propositions—we’re evaluating arguments here, and by definition those are just sets of propositions—but since classes are the fundamental logical unit, Aristotle restricts himself to a particular kind of proposition: categorical propositions. ‘Category’ is just a synonym of ‘class’. Categorical propositions are propositions that make a claim about the relationship between two classes. This is the first step in taming natural language: Aristotelian Logic will only evaluate arguments made up entirely of categorical propositions. The specific type of arguments it deals with are called syllogisms. We’re limiting ourselves to a restricted portion of language—sentences expressing these kinds of propositions, which will feature two class terms—terms picking out the classes whose relationship is described in the categorical proposition. Soon, we will place further restrictions on the forms these sentences can take, but for now we will discuss categorical propositions generally.

Again, categorical propositions make an assertion about the relationship between two classes. There are three possibilities here:

(1) Whole Inclusion: one class is contained entirely within the other.

Example: Class 1 = people; Class 2 = bipeds. The first class is entirely contained in the second; every person is a biped.

(2) Partial Inclusion: one class is partially contained within the other; the two classes have at least one member in common.

Example: Class 1 = people; Class 2 = swimmers. Some people swim; some don’t. Some swimmers are people; some aren’t (fish, e.g.). These two classes overlap, but not entirely.

(3) Exclusion: the two classes don’t have any members in common; they are exclusive. Example: Class 1 = people; Class 2 = birds. No people are birds; no birds are people. Batman notwithstanding (dude’s not really a bat; also, bats aren’t birds; robins are, but again, Robin’s not actually a bird, just a guy who dresses up like one).

Given these considerations, we can (more or less) formally define categorical propositions:

A categorical proposition is a claim about the relationship between two classes—call them S and P — that either affirms or denies that S is wholly or partially included in P.

Aristotle noted that, given this definition, there are four types of categorical proposition. We will discuss them in turn.

The Four Types of Categorical Proposition

Universal affirmative (A)

This type of proposition affirms the whole inclusion of the class S in the class P—it says that each member of S is also a member of P. The canonical expression of this proposition is a sentence of the form ‘All S are P’.

It is worth noting at this point why we chose ‘S’ and ‘P’ as the symbols for generic class terms. That’s because the former is the grammatical subject (S) of the sentence, and the latter is the grammatical predicate (P). This pattern will hold for the other three types of categorical proposition.

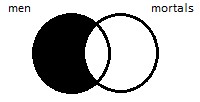
Back to the universal affirmative, A proposition. It affirms whole inclusion. For example, the sentence ‘All men are mortals’ expresses a proposition of this type, one that is true. ‘All men are Canadians’ also expresses a universal affirmative proposition, one that is false.

For the sake of concreteness, let’s choose subject and predicate classes that we can use as go-to examples as we talk about each of the four types of categorical proposition. Let’s let S = logicians and P = Germans. The A proposition featuring these two classes is expressed by ‘All logicians are germans’. (We’ll remain agnostic about whether it’s true or false.)

When it comes time to test arguments for validity—the last step in the process we’ve just begun— it will be convenient for us to represent the four types of categorical propositions pictorially. The basic form of the pictures will be two overlapping circles, with the left-hand circle representing the subject class and the right-hand circle representing the predicate class. Like this:

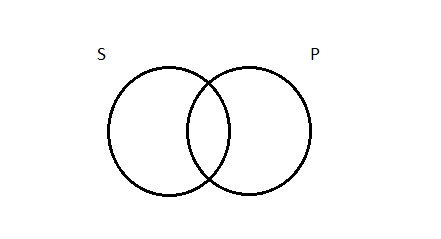
To depict the four types of categorical propositions, we’ll modify this basic two-circle diagram by shading in parts of it or making marks inside the circles.

Before we get to the specific depiction of the A proposition, though, let’s talk about what the basic two-circle diagram does. It divides the universe into four regions, to which we can assign numbers like this:

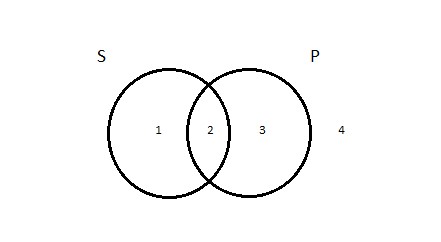
Let’s talk about what’s inside each of the four regions if we take S to be the class of logicians and P to be the class of Germans.

Region 1 is the portion of the S circle that doesn’t overlap with the P circle. These are things in the subject class but outside the predicate class; they are logicians who aren’t Germans. Aristotle was Greek, not German. So Aristotle is one of the residents of region 1—a logician who’s not a German.

Region 2 is the area of overlap between the subject and predicate classes; its residents are members of both. So here we have the logicians who are also Germans. Gottlob Frege, a 19^th century German logician, is the most important innovator in the history of logic other than Aristotle. He was German. So Frege lives in region 2; he’s both a logician and a German.

Region 3 is the portion of the P circle that doesn’t overlap with S. These are members of the predicate class—Germans, in our example—who are not members of the subject class—not logicians. This is where the non-logician Germans live. Wagner is a resident of region 3. The guy is clearly a German — but not a logician.

Region 4 is—everything else. It’s all the things that are outside both the subject and predicate classes—things that are neither logicians nor Germans. You know who isn’t German, but isn’t a logician, either? Beyoncé. She lives in region 4. But so do lots and lots and lots of other things: the planet Jupiter is neither a logician nor a German; it’s in there with Beyoncé, too. As is the left-front tire of my wife’s car. And the second-smallest brick in the Great Wall of China. And so on.

So much for the blank two-circle diagram and how it carves up the universe. What we want to figure out is how to alter that diagram so that we end up with a picture of the universal affirmative proposition. Our particular example of an A proposition is that all logicians are Germans. How do we draw a picture of that, using the two circles as our starting point? Well, think about it this way: when we say all logicians are Germans, what we’re really saying is that a certain kind of thing doesn’t exist; there’s no such thing as a non-German logician. In other words, despite what I said above about Aristotle, region 1 is empty, according to this proposition (which, again, may or may not be true; it doesn’t matter whether it’s true or not; we’re just trying to figure out how to draw a picture that captures the claim it makes). To depict emptiness, we will adopt the convention of shading in the relevant region(s) of the diagram. So our picture of the universal affirmative looks like this:

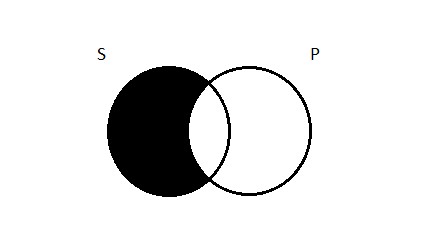
All S are P means that you won’t find any members of S that are outside the P circle (no logicians who aren’t Germans). The place in the diagram where they might’ve been such things is blotted out to indicate its emptiness. The only portion of S that remains as a viable space is inside the P circle, in what we called region 2 (the logicians you do find will all be Germans).

A reasonable question could be raised at this point: why did we draw the universal affirmative that way, instead of another, alternative and possibly more intuitive way? A propositions affirm whole inclusion—that S in entirely contained within P. Isn’t the obvious way to depict that state of affairs more like this:

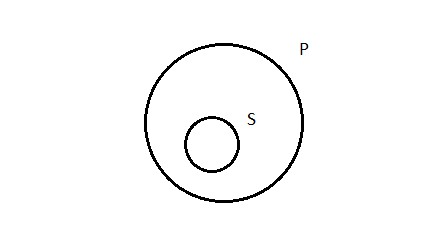
S entirely contained within P. Easy. Why bother with the overlapping circles and the shading?

There’s nothing wrong with this alternative depiction of the universal affirmative; it captures the claim being made. We adopt the first alternative depiction for purely practical reasons: when it comes time to test arguments for validity, we’re going to use these pictures; and our method will depend on our four types of categorical propositions all being depicted starting with the same basic two-overlapping-circle diagram, with shading and marks inside. These diagrams, as you may know, are called “Venn Diagrams”. They are named after the 19^th century English logician John Venn, who invented them specifically as an easier means of testing arguments for validity in Aristotelian Logic (things were more unwieldy before Venn’s innovation). It turns out Venn’s method only works if we start with the overlapping circles for all four of the types of categorical proposition. So that’s what we go with.

Universal negative (E)

This type of proposition denies that S is even partially included in P. Put another way: it affirms that S and P are exclusive—that they have no members in common. The canonical expression of this proposition is a sentence of the form ‘No S are P’. So, for example, the sentence ‘No dogs are cats’ expresses a true universal negative proposition; the sentence ‘No animals are cats’ expresses a false one.

Again, we want to think about how to depict this type of proposition using the standard two-circle Venn diagram. Think about the proposition that no logicians are Germans. How do we draw a picture of this claim? Well, as we said, E propositions tell us that the two classes don’t have any members in common. The region of the two-circle diagram where there are members of both classes is the area of overlap in the picture (what we referred to as region 2 above). The universal negative proposition tells us that there’s nothing in there. So if I claim that no logicians are Germans, I’m saying that, contrary to my claims above about the German-ness of Gottlob Frege, no, there’s no such thing as a logician-German. Region two is empty, and so we shade it out:

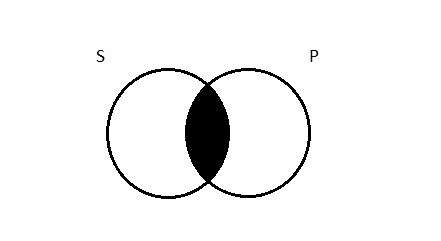
Particular affirmative (I)

This type of proposition affirms that S is partially included in P. Its canonical expression is a sentence of the form ‘Some S are P’. So, for example, ‘Some sailors are pirates’ expresses a true particular affirmative proposition; ‘Some sumo wrestlers are pigeons’ expresses a false one.

Before we talk about how to depict I propositions with a Venn diagram, we need to discuss the word ‘some’. Remember, in Aristotelian Logic we’re taming natural language by restricting ourselves to a well-behaved portion of it—sentences expressing categorical propositions. We’re proposing to use sentences with the word ‘some’ in them. ‘Some’, however, is not particularly well-behaved, and we’re going to have to get it in line before we proceed.

Consider this utterance: “Some Republican voters are gun owners.” This is true, and it communicates to the listener the fact that there’s some overlap between the classes of Republican voters and gun owners. But it also communicates something more—namely, that some of those Republicans aren’t gun owners. This is a fairly typical implicature (recall our discussion of this linguistic phenomenon in Chapter 2, when we looked at the fallacy of equivocation): when we say that some are, we also communicate that some are not.

But there are times when we use ‘some’ and don’t implicate that some are not. Suppose you’re talking to your mom, and you mention that you’re reading a logic book. For some reason, your mom’s always been curious about logic books, and asks you whether they’re a good read. You respond, “Well, mom, I can tell you this for sure: Some logic books are boring. You should see this book I’m reading now; it’s a total snooze-fest!” In this case, you say that some logic books are boring based on your experience with this particular book, but you do not implicate that some logic books are not boring; for all you know, all logic books are boring—it’s just impossible to write an exciting logic book. This is a perfectly legitimate use of the word ‘some’, where all it means is that there is at least one: when you utter ‘some logic books are boring’, all you communicate is that there is at least one boring logic book.

This is a bit of natural-language unruliness that we must deal with: sometimes when we use the word ‘some’, we implicate that some are not; other times, we don’t, only communicating that at least one is. When we use ‘some’ in Aristotelian Logic, we need to know precisely what’s being said. So we choose: ‘some’ means ‘there is at least one’. ‘Some S are P’ tells us that those two classes have at least one member in common, and nothing more. ‘Some sailors are pirates’ means that there’s at least one sailor who’s also a pirate, and that’s it. There is no implication that some sailors are not pirates; at least one of them is, and for all we know, all of them are.

This can confuse people, so it’s worth repeating. Heck, let’s indent it:

‘Some’ means ‘there is at least one’, and that’s it. It does not imply that some aren’t.

With that out of the way, we can turn our attention to the Venn diagram for the particular affirmative. It makes the assertion that S and P have at least one member in common. Turning to our concrete example, the sentence ‘Some logicians are Germans’ makes the claim that there is at least one logician who is a German. How do we draw a picture of this? We need to indicate that there’s at least one thing in the area of overlap between the two circles on the diagram—at least one thing inside of region 2. We do this by drawing an X:

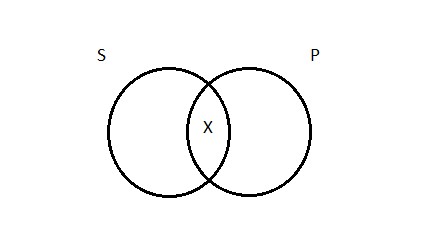
Particular negative (O)

This type of proposition denies that S is wholly included in P. It claims that there is at least one member of S that is not a member of P. Given that ‘some’ means ‘there is at least one’, the canonical expression of this proposition is ‘Some S are not P’—there’s at least one member of S that the two classes do not have in common. ‘Some sailors are not pirates’ expresses a true particular negative proposition; ‘Some dogs are not animals’ expresses a false one.

The Venn diagram for O propositions is simple. We need to indicate, on our picture, that there’s at least one thing that’s inside of S, but outside of P. To depict the fact that some logicians are not jerks, we need to put Aristotle (again, not a German, I’m pretty sure) inside the S circle, but outside the P circle. As with the diagram for the I proposition, we indicate the existence of at least one thing by drawing an X in the appropriate place:

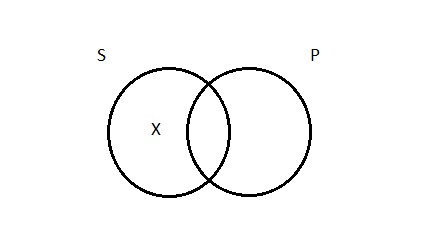
A Note on Terminology

It is commonly said that the four types of categorical propositions each have a quantity and a quality. There are two quantities: universal and particular. There are two qualities: affirmative and negative. There are four possible combinations of quantity and quality, hence four types of categorical proposition.

The universal propositions—A and E, affirmative and negative—are so-called because they each make a claim about the entire subject class. If I claim that all hobos are whiskey drinkers, I’ve made an assertion that covers every single hobo, every member of that class. Similarly, if I claim that no chickens are race car drivers, I’ve made an assertion covering all the chickens—they all fail to drive race cars.

The particular propositions—I and O, affirmative and negative— on the other hand, do not make claims about every member of the subject class. ‘Some dinosaurs were herbivores’ just makes the claim that there was at least one plant-eating dinosaur; we don’t learn about all the dinosaurs. Similar remarks apply to an O proposition like ‘Some dinosaurs were not carnivores’. Remember, ‘some’ just means ‘at least one’.

The affirmative propositions—A and I, universal and particular—make affirmative claims about the relationship between two classes. A propositions affirm whole inclusion; I propositions affirm partial inclusion. Trivial fact: the Latin word meaning ‘I affirm’ is affirmo; the A and the I in that word are where the one-letter nicknames for the universal and particular affirmatives come from.

The negative propositions—E and O, universal and particular—make negative claims about the relationship between two classes. E propositions deny even partial inclusion; O propositions deny whole inclusion. Trivial fact: the Latin word meaning ‘I deny’ is nego; the E and the O in that word are where the one-letter nicknames for the universal and particular negatives come from.

Standard form for Sentences Expressing Categorical Propositions

To tame natural language, Aristotelian Logic limits itself to that portion of language that expresses categorical propositions. Above, we gave “canonical” sentences for each of the four types of categorical proposition: ‘All S are P’ for the universal affirmative; ‘No S are P’ for the universal negative; ‘Some S are P’ for the particular affirmative; and ‘Some S are not P’ for the particular negative. These are not the only ways of expressing these propositions in English, but we will restrict ourselves to these standard forms. That is, we will only evaluate arguments whose premises and conclusion are expressed with sentences with these canonical forms.

Generally speaking, here is the template for sentences qualifying as standard form:

[Quantifier] Subject Term <copula> (not) Predicate Term

Standard form sentences begin with a quantifier—a word that indicates the quantity of the categorical proposition expressed. Restriction: only sentences beginning with ‘All’, ‘No’, or ‘Some’ qualify as standard form.

Subject and predicate terms pick out the two classes involved in the categorical proposition. Restriction: subject and predicate terms must be nouns or noun-phrases (nouns with modifiers) in order for a sentence to be in standard form.

The copula is a version of the verb ‘to be’ (‘are’, ‘is’, ‘were’, ‘will be’, etc.). Degree of freedom: it doesn’t matter which version of the copula occurs in the sentence; it may be any number or tense. ‘Some sailors are pirates’ and ‘Some sailors were pirates’ both count as standard form, for example.

The word ‘not’ occurs in the standard form expression of the particular negative, O proposition: ‘Some sailors are not pirates’. Restriction: the word ‘not’ can only occur in sentences expressing O propositions; ‘not’ appearing with any quantifier other than ‘some’ is a deviation from standard form.

We now have a precise delimitation of the portion of natural language to which Aristotelian Logic restricts itself: only sentences in standard form. But now a worry that we raised earlier becomes acute: if we can only evaluate arguments whose premises and conclusions are expressed with standard form sentences, aren’t we severely, perhaps ridiculously, constrained? Has anyone, ever, outside a logic book, expressed a real-life argument that way?

This is where translation comes in. Lots of sentences that are not in standard form can be translated into standard form sentences that have the same meaning. Aristotle himself believed that all propositions, no matter how apparently complex or divergent, could ultimately be analyzed as one of the four types of categorical proposition. Though this is, to put it mildly, not a widely held belief today, it still had an enormous influence in the history of logic, since Aristotle’s system was preeminent for more than 2,000 years. Over that time, logicians developed ever more elaborate procedures for analyzing a dizzying variety of non-Standard form sentences as expressing one of the four types of categorical propositions, and translating them accordingly. An exhaustive survey of those inquiries would be exhausting, and beyond the scope of this book. It will be enough to look at a few simple examples to get an idea of how many apparently deviant expressions can be treated by Aristotelian Logic. Our goal is simply to allay concerns that in restricting ourselves to standard form sentences we are severely limiting our logic’s power to evaluate real-life arguments.

Let’s consider the first deductively valid argument we encountered in this book, the one about Socrates: All men are mortal; Socrates is a man; therefore, Socrates is mortal. This argument has three propositions in it, but none of the three sentences expressing them are in standard form. The first sentence, ‘All men are mortal’, may appear to fit the bill, but it has a subtle flaw: ‘mortal’ is an adjective, not a noun. Class terms are required to be nouns or noun phrases. But this is an easy fix: add an ‘s’ to the end and you get a plural noun. ‘All men are mortals’ is in standard form; it expresses a universal affirmative, A proposition. This prescription applies generally. Predicate adjectives can be replaced with suitable noun phrases most easily by just inserting the generic noun ‘things’: ‘Some men are handsome’ becomes ‘Some men are handsome things’; ‘No priests are silly’ becomes ‘No priests are silly things’.

Back to the Socrates argument. The second premise is also problematic: ‘Socrates is a man’. First of all, it doesn’t have a quantifier. Second, its subject term, ‘Socrates’, picks out an individual person; we’re supposed to be dealing with classes here, right? Well, that’s right, but it’s not really a problem. We can just make the subject class a unit class—a class containing exactly one member, namely Socrates. Now we can understand the sentence as expressing the claim that the single member of that class is also a member of the class of men. That is, it’s a universal affirmative— there’s whole inclusion of the Socrates unit-class in the class of men. The sentence we need, then, starts with the quantifier ‘All’, and to make the grammar work, we pick a plural noun to name the Socrates class: ‘All Socrateses are men’. Is ‘Socrateses’ the plural of ‘Socrates’? I can’t think of anything better. Anyway, the point is, that word picks out a class that has exactly one member, Socrates. Sentences with singular subjects can be rendered as universals. If I had the sentence ‘Socrates is not alive’, I could render it as a universal negative: ‘No Socrateses are living things’.

There are other things to consider. English comes with a variety of quantifier words: ‘each’, ‘every’, ‘any’, and so on. Common sense tells us how to translate sentences featuring these into standard form: switch to the appropriate standard form quantifier—‘All’, ‘No’, or ‘Some’. ‘Every teacher is a hard worker’ becomes ‘All teachers are hard workers’, for example. Sometimes quantifier words are omitted, but it’s clear from context what’s going on. ‘Dogs are animals’ means ‘All dogs are animals’; ‘People are waiting in line’ can be rendered as ‘Some people are things that are waiting in line’. Some sentences have a verb other than the copula. ‘Some people eat rabbit’, for example, can be translated into ‘Some people are rabbit-eaters’. Sometimes the word ‘not’ appears in a sentence that has a quantifier other than ‘some’. ‘Not all mammals are carnivores’, for example, can be translated into ‘Some mammals are not carnivores’.

The list goes on. As I said, centuries of work has been done on the task of translating sentences into standard form. We can stop here, I think, and simply accept that the restriction to standard form sentences does not seriously limit the arguments that Aristotelian Logic can evaluate.

III. The Square of Opposition

Having established the boundaries of our domain of logically well-behaved natural language, we turn now to an investigation of the properties of its inhabitants. The four types of categoricals are related to one another in systematic ways; we will look at those relationships.

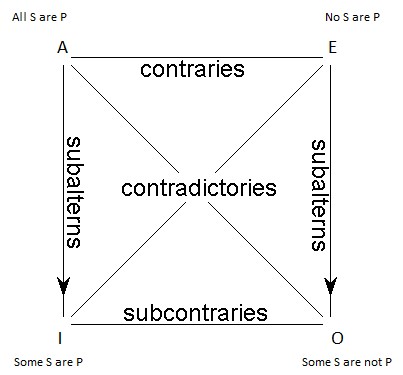
The relationships are inferential: we can often infer, for example, from the truth of one of the four categoricals, whether the other three are true or false. These inferential relationships among the four categorical propositions are summarized graphically in a diagram: The Square of Opposition. The diagram looks like this:

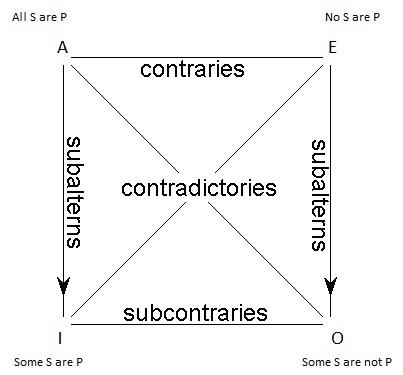
The four types of categorical propositions are arranged at the four corners of the square, and along the sides and diagonals are marked the relationships that obtain between pairs of them.

Now the Square of Opposition has a funny history. As we shall see, it involves some hidden commitments to what certain words, especially “some” entail. In fact, although Aristotle and the logical system that bears his name followed this square for nearly 2,000 years, there are now parts of the square to which we no longer adhere. Section V discusses these new changes and how such changes affect the types of inferences we can make with the square and categorical propositions, in general.

However, the classic Square of Opposition still provides a great way to explore potential relationships between categorical propositions in a graphic manner. Being able to follow along with these potential relationships, even if we adjust them down the road, can help us become more comfortable manipulating the ideas behind A, E, I, and O propositions. And so, it is to these relationships that we will now turn.

Contradictories

Contradictory pairs of categorical propositions are at opposite corners from one another on the Square of Opposition. A and O propositions are contradictory; E and I propositions are contradictory. What it means for a pair of propositions to be contradictory is this: they have opposite truth-values; when one is true, the other must be false, and vice versa.

This is pretty intuitive. Consider an A proposition—all sailors are pirates. Suppose I make that claim. How do you contradict me? How do you prove I’m wrong? “My brother’s in the Navy,” you might protest. “He’s a sailor, but he’s not a pirate.” That would do the trick. The way you contradict a universal affirmative claim—a claim that all S are P—is by showing that there’s at least one S (a sailor in this case, your brother) who’s not a P (not a pirate, as your brother is not). At least one S that’s not a P—that’s just the particular negative, O proposition, that some S are not P. (Remember: ‘some’ means ‘there is at least one’.) A and O propositions make opposite, contradictory claims. If it’s false that all sailors are pirates, then it must be true that some of them aren’t; that’s just how you show it’s false. Likewise, if it’s true that all dogs are animals (it is), then it must be false that some of them are not (you’re not going to find even one dog that’s not an animal). A and O propositions have opposite truth-values.

Likewise for E and I propositions. If I claim that no saints are priests, and you want to contradict me, what you need to do is come up with a saint who was a priest. It’s not hard: Saint Thomas Aquinas (who was the most prominent medieval interpreter of Aristotle, by the way, and a terrific philosopher in his own right) was a priest. So, to contradict universal negative claim—that no S are P—you need to show that there’s at least one S (a saint in this case, Thomas Aquinas) who is in fact a P (a priest, as Aquinas was). At least one S that is a P—that’s just the particular affirmative, I proposition, that some S are P. (Again, ‘some’ means ‘there is at least one’.) E and I propositions make opposite, contradictory claims. If it’s false that no saints are priests, it must be true that some of them are; that’s just how you show it’s false. Likewise, it’s true that no cats are dogs (it is), then it must be false that some of them are (you’re not going to find even one cat that’s a dog). E and I propositions have opposite truth-values.

Contraries

The two universal propositions—A and E, along the top of the Square—are a contrary pair. This is a slightly weaker form of opposition than being contradictory. Being contrary means that they can’t both be true, but they could both be false—though they needn’t both be false; one could be true and the other false.

Again, this is intuitive. Suppose I claim the universal affirmative, “All dogs go to heaven,” and you claim the corresponding universal negative, “No dogs go to heaven.” (Those sentences aren’t in standard form, but the translation is easy.) Obvious observation: we can’t both be right; that is, both claims can’t be true. On the other hand, we could both be wrong. Suppose getting into heaven, for dogs, is the way they say it is for people: if you’re good and stuff, then you get in; but if you’re bad, oh boy—it’s the Other Place for you. In that case, both of our claims are false: some dogs (the good ones) go to heaven, but some dogs (the bad ones, the ones who bite kids, maybe) don’t. But that picture might be wrong, too. I could be right and you could be wrong: God loves all dogs equally and they get a free pass into heaven. Or, I could be wrong and you could be right: God hates dogs and doesn’t let any of them in; or maybe there is no heaven at all, and so nobody goes there, dogs included.

Subcontraries

Along the bottom of the Square we have the two particular propositions—I and O—and they are said to be subcontraries. This means they can’t both be false, but they could both be true—though they needn’t be; one could be true and the other false.

It’s easy to see how both I and O could be true. As a matter of fact, some sailors are pirates. That’s true. Also, as a matter of fact, some of them are not. It’s also easy to see how one of the particular propositions could be true and the other false, provided we keep in mind that ‘some’ just means ‘there is at least one’. It’s true that some dogs are mammals—that is, there is at least one dog that’s a mammal—so that I proposition is true. In fact, all of them are—the A proposition is true as well. Which means, since A and O are contradictories, that the corresponding O proposition—that some dogs are not mammals—must be false. Likewise, it’s true that some women are not (Catholic) priests (at least one women isn’t a priest); and it’s false that some women are priests (the Church doesn’t allow it). So O can be true while I is false.

It’s a bit harder to see why both particular propositions can’t be false. Why can’t ‘Some surfers are priests’ and ‘Some surfers are not priests’ both be false? It’s not immediately obvious. But think it through: if the I (some surfers are priests) is false, that means the E (no surfers are priests) must be true, since I and E are contradictory; and if the O (some surfers are not priests) is false, that means the A (all surfers are priests) must be true, since O and A are contradictory. That is to say, if I and O were both false, then the corresponding A and E propositions would both have to be true. But, as we’ve seen already, this is (obviously) impossible: if I claim that all surfers are priests and you claim that none of them are, we can’t both be right.

Subalterns

The particular propositions at the bottom of the table—I and O—are subalterns of the universal propositions directly above them—A and E, respectively.^[1] This means that the pairs have the following relationship: if the universal proposition is true, then the particular proposition (its subaltern) must also be true. That is, if an A propositions is true, it’s corresponding I proposition must also be true; if an E proposition is true, its corresponding O proposition must also be true.

This is intuitive if we keep in mind, as always, that ‘some’ means ‘there is at least one’. Suppose the A proposition that all whales are mammals is true (it is); then the corresponding I proposition, that some whales are mammals, must also be true. Again, ‘some whales are mammals’ just means ‘at least one whale is a mammal’; if all of them are, then at least one of them is! Similarly, on the negative side of the square, if it’s true the no priests are women (universal negative, E), then it’s got to be true that some priests are not women (particular negative, O)—that at least one priest is not a woman. If none of them are, then at least one isn’t!

Notice that these relationships are depicted in a slightly different way from the others on the Square of Opposition: there’s an arrow pointing toward the bottom. This is because the relationship is not symmetrical. If the proposition on top is true, then the one on the bottom must also be true; but the reverse is not the case. If an I proposition is true—some sailors are pirates—it doesn’t follow that the corresponding A proposition—that all sailors are pirates—is true. Likewise, the truth of an O proposition—some surfers are not priests—does not guarantee the truth of the corresponding E proposition—that no surfers are priests.

Truth, as it were, travels down the side of the Square. Falsehood does not: if the universal proposition is false, that doesn’t tell us anything about the truth or falsehood of the corresponding particular. You could have a false A proposition—all men are priests—with a true corresponding I—some men are priests. But you could also have a false A proposition—all cats are dogs—whose corresponding I—some cats are dogs—is also false. Likewise, you could have a false E proposition—no men are priests—with a true corresponding O—some men are not priests. But you could also have a false E proposition—no whales are mammals—whose corresponding O— some whales are not mammals—is also false.

Falsehood doesn’t travel down the side of the Square, but it does travel up. That is, if a particular proposition—I or O—is false, then its corresponding universal proposition—A or E, respectively—must also be false. Think about it in the abstract: if it’s false that some S are P, that means that there’s not even on S that’s also a P; well in that case, there’s no way all the Ss are Ps! False I, false A. Likewise on the negative side: if it’s false that some S are not P, that means you won’t find even one S that’s not a P, which is to say all the Ss are Ps; in that case, it’s false that no S are P (A and E are contraries). False O, false E.

Inferences

Given information about the truth or falsity of a categorical proposition, we can use the relationships summed up in the Square of Opposition to make inferences about the truth-values of the other three types of categorical proposition.

Here’s what I mean. Suppose a universal affirmative proposition—an A proposition—is true. What are the truth-values of the corresponding E, I, and O propositions? (By “corresponding”, I mean propositions with the same subject and predicate classes.) The Square can help us answer these questions. First of all, A is in the opposite corner from O—they’re contradictory. That means A and O have to have opposite truth-values. Well, if A is true, as we’re supposing, then the corresponding O proposition has to be false. Also, A and E are contraries. That means that they can’t both be true. Well, we’re supposing that the A is true, so then the corresponding E must be false. What about the I proposition? Three ways to attack this one, and they all agree that the I must be true: (1) I is the subaltern of A, so if A is true, then I must be true as well; (2) I is the contradictory of E, and we’ve already determined that E must be false, so I must be true; (3) I and O are subcontraries, meaning they can’t both be false, and since we’ve already determined that O is false, it follows that I must be true.

Summing up: if an A proposition is true, the corresponding E is false, I is true, and O is false.

Let’s try another one: suppose a universal negative, E proposition is true. What about the corresponding A, I, and O propositions? Well, again, A and E are contraries—can’t both be true— so A must be false. I is the contradictory of E, so it must be false—the opposite of I’s truth-value. And since O is subaltern to E, it must be true because E is.

If an E proposition is true, the corresponding A is false, I is false, and O is true.

Another. Suppose a particular affirmative, I proposition is true. What about the other three? Well, E is its contradictory, so it must be false. And if some S are P, that means some of them aren’t— so the O is also true. And since A is the contradictory of O… WAIT JUST A MINUTE! Go back and read that again. Do you see what happened? “And if some S are P, that means some of them aren’t….” No it doesn’t! Remember, ‘some’ means ‘there is at least one’. If some S are P, that just means at least one S is a P—and for all we know, all of them might be; and then again, maybe not. I and O are subcontraries: they can’t both be false, they could both be true, and one could be true and the other false. Knowing that I is true tells us nothing about the truth-value of the corresponding O, or the corresponding A. That some are, meaning at least one is, leaves open the possibility that all of them are; but then again, maybe not. The fact is, based on the supposition that an I is true, we can only know the truth-value of the corresponding E for sure.

If an I proposition is true, then the corresponding E is false, and A and O are of unknown truth value.

EXERCISES

1. Suppose an O proposition is true. What are the truth-values of the corresponding A, E, and I propositions, according to the Square of Opposition?
2. Suppose an A proposition is false. What are the truth-values of the corresponding E, I, and O propositions, according to the Square of Opposition?
3. Suppose an E proposition is false. What are the truth-values of the corresponding A, I, and O propositions, according to the Square of Opposition?
4. Suppose an I proposition is false. What are the truth-values of the corresponding A, E, and O propositions, according to the Square of Opposition?
5. Suppose an O proposition is false. What are the truth-values of the corresponding A, E, and I propositions, according to the Square of Opposition?

IV. Operations on Categorical Sentences

We continue our exploration of the portion of natural language to which Aristotle’s logic restricts itself—the standard form sentences expressing categorical propositions. To familiarize ourselves more intimately with these, we will look at how they respond when we perform various operations on them, when we manipulate them in various ways. We will examine three operations: conversion, obversion, and contraposition. Each of these alters the standard form sentences in some way. The question we will ask is whether the new sentence that results from the manipulation is equivalent to the original sentence; that is, does the new sentence express the same proposition as the original?

Conversion

Performing conversion on a categorical sentence involves changing the order of the subject and predicate terms. The result of this operation is a new sentence, which is said to be the converse of the original sentence. Our question is: when does performing conversion produce an equivalent new sentence, a converse that expresses the same proposition as the converted original? We will look at all four types standard form sentence, answering the question for each.

Let’s perform conversion on a sentence expressing a universal affirmative, A proposition and see what happens. ‘All dogs are animals’ is such a sentence. conversion switches the subject and predicate terms, so the converse sentence is ‘All animals are dogs’. Does the converse express the same proposition as the original? Are they equivalent? Heck, no! The original sentence expresses the true proposition that all dogs are animals; the converse expresses the utterly false proposition that all animals are dogs. Converting an A sentence produces a new sentence that is not equivalent to the original.

This means that the effect on truth-value, in the abstract, of converting A sentences, is unpredictable. Sometimes, as with ‘All dogs are animals’, conversion will lead you from a truth to a falsehood. Other times, it may lead from truth to truth: ‘All bachelors are unmarried men’ and ‘All unmarried men are bachelors’ express different propositions, but both of them are true (because it so happens that, by definition, a bachelor is just an unmarried man). conversion of an A could also lead from falsehood to falsehood, as with the transition from ‘All dogs are bats’ to ‘All bats are dogs’. And it could lead from falsehood to truth: just reverse the order of the first conversion we looked at, from ‘All animals are dogs’ to ‘All dogs are animals’.

Again, the point here is that, because conversion of A sentences produces a converse that expresses a different proposition than the original, we cannot know what the effect of the conversion will be on truth-value.

How about conversion of sentences expressing universal negative, E propositions? ‘No dogs are cats’ is such a sentence. Its converse would then be ‘No cats are dogs’. Are they equivalent? Yes, of course. Remember, an E proposition denies even partial inclusion; it makes the claim that the two classes involved don’t have any members in common. It doesn’t matter which of the two classes is listed first in the sentence expressing that proposition—you still get the assertion that the two classes are exclusive. This is true of E sentences generally: performing conversion on them always produces a new sentence that is equivalent to the original.

It is also true of sentences expressing particular affirmative, I propositions. ‘Some sailors are pirates’, after conversion, becomes ‘Some pirates are sailors’. These express the same proposition: they make the claim that the two classes have at least one member in common—there is at least one thing that is both a sailor and a pirate. Again, it doesn’t matter what order you put the class terms in; I sentences express the assertion that there’s overlap between the two classes. An I sentence and its converse are always equivalent.

The same cannot be said of sentences expressing particular negative, O propositions. Consider ‘Some men are not priests’. That expresses a true proposition. But its converse, ‘Some priests are not men’ expresses a different proposition; we know it’s a different proposition because it’s false. That is all we need to show that an operation does not produce equivalent sentences: one counterexample. As above with A sentences, this means that the effect on truth-value of converting O sentences is unpredictable. It can take us from truth to falsehood, as in this example, or from truth to truth, falsehood to falsehood, falsehood to truth. In the abstract, we cannot know the effect on truth of converting O sentences, since the converse expresses a different proposition from the original.

Summary for conversion: for E and I, converses are equivalent; for A and O, converses are not.

Obversion

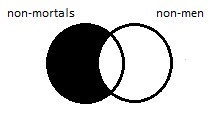
Before we talk about our next operation, obversion, we need to introduce a new concept: class complements. The complement of a class, call it S, is another class which contains all the things that are not members of S. So, for example, the complement of the class of trees is just all the things that aren’t trees. The easiest way to name class complements is just to stick the prefix ‘non’ in front of the original class name. So the complement of trees is non-trees. Be careful: it may be tempting, for example, to say that the complement of Republicans is Democrats. But that’s not right. The complement of Republicans is a much bigger class, containing all the non-Republicans: not just Democrats, but Communists and Libertarians and Independents and Greens; oh, and a bunch of other things, too—like the planet Jupiter (not a Republican), my left pinkie toe, the Great Wall of China, etc., etc.

As a matter of notational convention, if we use a capital letter like S to refer to a class, we will denote the complement of that class as ~ S, which we’ll read as “tilde-S.”

Back to obversion. Here’s how this operation works: first, you change the quality of the sentence (from affirmative to negative, or vice versa); then, you replace the predicate with its complement. The result of performing obversion on a sentence is called the obverse of the original.

It turns out that performing obversion on a sentence always produces a new sentence that’s equivalent to it; a sentence and its obverse always express the same proposition. That means they share a truth-value: if a sentence is true, so is its obverse; if a sentence is false, its obverse is false, too. We can see that this is so by looking at the result of performing obversion on each of the four types of standard form sentences.

We’ll start with A sentences. Consider ‘All ducks are swimmers’. To perform obversion on this sentence, we first change its quality. This is a universal affirmative. Its quality is affirmative. So we change that to negative, keeping the quantity (universal) the same. Our new sentence is going to be a universal negative, E sentence—something of the form No S are P. Next, we replace the predicate with its complement. The predicate of the sentence is ‘swimmers’. What’s the complement of that class? All the things that aren’t swimmers: non-swimmers. So the obverse of the original A sentence is this: ‘No ducks are non-swimmers’.

Now, are these two sentences equivalent? Yes. ‘All ducks are swimmers’ expresses the universal affirmative proposition, asserting that the class of ducks is entirely contained in the class of swimmers. That is to say, any duck you find will also be in the swimmer class. Another way of putting it: you won’t find any ducks who aren’t in the class of swimmers. In other words, no ducks fail to be swimmers. Or: ‘No ducks are non-swimmers’. The A sentence and its obverse are equivalent; they express the same proposition, make the same claim about the relationship between the class of ducks and the class of swimmers.

Let’s try obversion on a universal negative, E sentence. ‘No women are priests’ is one. First, we change its quality from negative to affirmative: it becomes a universal affirmative, A sentence— something of the form All S are P. Next, we replace it predicate, ‘priests’, with its complement, ‘non-priests’. The result: ‘All women are non-priests’. Is that equivalent to the original? It tells us that all women are outside the class of priests. In other words, none of them are priests. That is, ‘No women are priests’. Yes, both the original sentence and its obverse tell us that the classes of women and priests are exclusive.

Next, the particular affirmative—an I sentence like ‘Some politicians are Democrats’. OK. First, change the quality—from affirmative to negative. Our obverse will be a particular negative, O sentence—something of the form Some S are not P. Now, replace ‘Democrats’ with ‘nonDemocrats’, stick it in the predicate slot, and we get ‘Some politicians are not non-Democrats’. Well, that’s not exactly grammatically elegant, but the meaning is clear: not being a non-Democrat is just being a Democrat. This says the same are the original, namely that some politicians are Democrats.

Finally, particular negative, O. We’ll try ‘Some plants are not flowers’. Changing from negative to affirmative means our obverse will be an I—Some S are P. We replace ‘flowers’ with ‘nonflowers’ and get ‘Some plants are non-flowers’. We went from ‘Some plants are not flowers’ to ‘Some plants are non-flowers’. Obviously, those are equivalent.

Summary for obversion: obverses are equivalent for A, E, I, and O.

Contraposition

Our last operation is contraposition. Unlike obversion, and like conversion, it doesn’t involve changing the type (A, E, I, O) of the sentence we’re operating on. Rather, again, like conversion, we just manipulate the subject and predicate. Here’s how: replace the subject with the complement of the predicate; and replace the predicate with the complement of the subject. The result of performing contraposition on a sentence is called its contrapositive.

Let’s perform contraposition on an A sentence: ‘All men are mortals’. To form its contrapositive, we put the complement of the predicate—non-mortals—into subject position and the complement of the subject—non-men—into predicate position: ‘All non-mortals are non-men’. The question, as always: are these sentences equivalent? This one’s a bit hard to see. Let’s use Venn diagrams to help us think it through. First, we know what the diagram for ‘All men are mortals’ looks like; that sentence claims that there’s no such thing as a man who’s not a mortal, so we blot out the portion of the ‘men’ circle that’s not inside the ‘mortals’ circle:

Next, let’s think through how we would diagram ‘All non-mortals are non-men’. If we change our circles to ‘non-men’ and ‘non-mortals’, respectively, it’s easy; when you’re diagramming an A proposition, you just blot out the part of the left-hand (subject) circle that doesn’t overlap with the right-hand (predicate) circle. There’s no such thing as non-men who aren’t non-mortals:

But how do we compare this diagram with the one for ‘All men are mortals’ to see if they express the same proposition? We need to know that the two would give us the same picture if the circles were labeled the same.

Let’s compare the unshaded diagrams where the circles are ‘men’ and ‘mortals’, on the one hand, and ‘non-men’ and ‘non-mortals’ on the other:

When we depict ‘All men are mortals’, we blot out region 1 of the left-hand diagram. When we depict its contrapositive, ‘All non-mortals are non-men’, we blot out region w of the right-hand diagram. We want to know whether these two sentences are equivalent. They are, provided that blotting out region 1 and blotting out region w amount to the same thing. Do they? That is, do regions 1 and w contain the same objects?

Let’s think this through, starting with region z. What’s in there? Those are the things that are outside both the non-mortal and non-men circles; that is, they’re not non-mortals and they’re not non-men. So they’re mortals and men, right? Things that are both mortals and men: on the lefthand diagram, that’s the overlap between the circles. Region z and region 2 contain the same things.

How about region y? Those things are non-men, but they’re outside the non-mortals circle, making them mortals. Mortals who aren’t men: they live in region 3 in the left-hand diagram. Regions y and 3 contain the same things. Region x has things that are both non-men and non-mortals; that is, they’re outside both the mortal and men circles on the left. Regions x and 4 contain the same things.

And region w? Outside the non-men circle, so they’re men. Inside the non-mortals circle, so they’re not mortals. Men that aren’t mortals: that’s region 1 on the left. Regions w and 1 contain the same things. And that means that blotting out region w and blotting out region 1 amount to the same thing; both are ways of ruling out the existence of the same group of objects, the men who aren’t mortals—or, as it turns out, the non-mortals who aren’t non-men. Same thing.

Picking the main thread back up, what all this shows is that when we perform contraposition on universal affirmative, A sentences, we end up with new sentences that express the same proposition. An A sentence and its contrapositive are equivalent. We still have to ask the same question about E, I, and O sentences.

Consider a universal negative (E): ‘No sky-divers are cowards’. This is surely true; it takes bravery to jump out of a plane (I wouldn’t do it). To get the contrapositive, we replace the subject, skydivers, with the complement of the predicate, non-cowards; and we replace the predicate, cowards, with the complement of the subject, non-sky-divers. The result is ‘No non-cowards are non-skydivers’. That’s false. You know who was a non-coward? Martin Luther King, Jr. The Reverend King was a courageous advocate for racial equality up to the very last day of his life. But, not a sky-diver. The contrapositive claims there’s no such thing as a non-coward who doesn’t sky-dive. But that ain’t so: MLK is a counterexample. In general, when you perform contraposition on an E sentence, you end up with a new sentence that expresses a different proposition. And as was the case with A and O sentences being converted, this has unpredictable effects on truth-value. You may move from truth to falsehood, as in this case, or from truth to truth, falsehood to falsehood, falsehood to truth. Contraposition changes the proposition expressed by E sentences, so you can’t know.

Next, consider particular negative (O) sentences. These are pretty easy. ‘Some men are not priests’ is a good go-to example. Performing contraposition, we get ‘Some non-priests are not non-men’. Things that are not non-men—those are just men. So the claim being made by the contrapositive is that some non-priests are men. That is, there’s at least one thing that’s both a non-priest and a man; or, there’s at least one man who’s not a priest. I know a way to say that: ‘Some men are not priests’. The O sentence and its contrapositive make the same claim. Contraposition performed on particular negatives gives you a new sentence that is equivalent to the original.

Finally, particular affirmatives—I sentences. ‘Some men are priests’ is true. So is its contrapositive: ‘Some non-priests are non-men’ (there’s at least one: my mom is not a man, nor was she ever a priest). So contraposition performed on an I works? That is, it gives you an equivalent sentence? Not necessarily. The two sentences might both be true, but they could be expressing two different true propositions. As a matter of fact, they are. When you contrapose an I sentence, the result is a new sentence that is not equivalent. To see why, we’ll return to Venn diagrams.

Generically speaking, an I proposition’s diagram has an X in the area of overlap between the two circles. For a sentence of the form Some S are P, we would draw this:

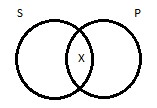
There is at least one thing (the X) that is both S and P. For the contrapositive, we draw this:

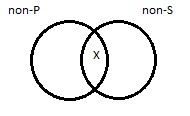
There is at least one thing that is both non-P and non-S. The question is, does drawing an X in those two regions of overlap amount to the same thing? Let’s put the diagrams side-by-side, without the Xs, but with numbers and letters for the different regions:

We went through this above when we were discussing the effects of contraposition on A propositions. Regions 1 and w contain the same things, as do regions 3 and y. But regions 2 and 4 don’t line up with regions x and z, respectively. Rather, they’re reversed: region 2 has the same objects as region z, and region 4 has the same objects as region x.

When we draw the picture of the straight-up I sentence, we put an X in region 2; when we draw the picture of its contrapositive, we put an X in region x. But region 2 and region x aren’t the same. So the I sentence and its contrapositive, in general, are not equivalent. Performing contraposition on an I sentence changes the proposition expressed, with unpredictable effects on truth-value.

We can prove it with a concrete example. Let our starting I sentence be ‘Some Catholics are nonPopes’. That’s certainly true (again, my mom: Catholic, but not Pope). The contrapositive would be ‘Some Popes are non-Catholics’ (the complement of non-Popes is just Popes). But that’s false. Being Catholic is a prerequisite for the Papacy. An I sentence and its contrapositive make different claims.

EXERCISES

1. Perform conversion on the following and write down the converse. Is it equivalent to the original sentence?

(a) Some surfers are not priests.

(b) All Canadians are bodybuilders.

(c) No Mexicans are fishermen.

(d) Some Nazis are florists.

2. Perform obversion on the following and write down the obverse. Is it equivalent to the original sentence?

(a) No people are lizards.

(b) Some politicians are criminals.

(c) Some birds are not animals.

(d) All Democrats are samurais.

3. Perform contraposition on the following and write down the contrapositive. Is it equivalent to the original sentence?

(a) All Philistines are Syrians.

(b) No Africans are Europeans.

(c) Some Americans are Irishmen.

(d) Some Swiss are not Catholics.

Inferences

Earlier, we discussed how we could make inferences about the truth-values of categoricals using the information encoded in the Square of Opposition. For example, given the supposition that an A sentence expresses a true proposition, we can infer that the corresponding E sentence expresses a falsehood (since A and E are contraries, which can’t both be true), that the corresponding I sentence expresses a truth (since I is the subaltern of A, which means A’s truth guarantees that of I), and that the corresponding O sentence expresses a falsehood (since A and O are contradictories, which must have opposite truth-values).

The key word in that paragraph is ‘corresponding’. The Square of Opposition tells us about the relationships among categoricals that correspond—which means they have the same subjects and predicates. If ‘All S are P’ is true, then ‘No S are P’ must be false, per the Square, since these two sentences have the same subject (S) and predicate (P). The square cannot license such inferences when the subjects and predicates do not correspond. The supposition that ‘All S are P’ is true tells me nothing at all about the truth-value of ‘Some A are B’; the subjects and predicates are different; we’re dealing with two different classes.

There are occasions, however, when subjects and predicates do not correspond, but we can nevertheless make inferences about the truth-values of categoricals based on information about others. In such cases, we need to combine our knowledge of the relationships depicted in the Square of Opposition with our recently acquired knowledge about the circumstances in which conversion, obversion, and contraposition provide us with equivalent sentences.

Here is a simple example. Suppose that a sentence of the form ‘No S are P’ expresses a truth (never mind what ‘S’ and ‘P’ stand for; we’re thinking in the abstract here). Given that information, what can we say about a sentence of the form ‘Some P are S’? Well, the first is an E and the second is an I. According to the Square of Opposition, E and I are a contradictory pair, so they must have opposite truth-values. But remember, the relationships in the Square only hold for corresponding sentences. ‘No S are P’ and ‘Some P are S’ do not correspond; their subject and predicate class terms are in different spots. The Square tells us that the I sentence corresponding to ‘No S are P’— namely, ‘Some S are P’—must be the opposite truth-value. We’ve presumed that the E sentence is true, so ‘Some S are P’ expresses a falsehood, according to the Square. But we wanted to know the truth-value of ‘Some P are S’, the sentence with the subject and predicate terms switched. Well, switched subject and predicate terms—that’s just the converse of ‘Some S are P’. And we know from our investigations that performing conversion on an I sentence always gives you another I sentence that’s equivalent to the first; that is, it expresses the same proposition, so it’s true or false in all the same circumstances as the original. That means ‘Some P are S’ must express a falsehood, just like its converse.

Here’s how to think about the inference we just made. We were given the fact that ‘No S are P’ is true. We wanted to know the truth-value of ‘Some P are S’. We can’t compare these two directly using the Square of Opposition because they don’t correspond: different subject and predicate. But, we know that the converse of the our target sentence—‘Some S are P’—does correspond, so according to the Square, it must be false (since it’s contradictory to ‘No S are P’). And, since conversion on I sentences yields equivalent results, ‘Some P are S’ has the same truth-value as ‘Some S are P’, so our target sentence must also be false.^[2]

This is the general pattern for these sorts of multi-step inferences. You’re given information about a particular categorical claim’s truth-value, then asked to evaluate some other claim for truth or falsity. They may not correspond, so the first stage of your deliberations involves getting them to correspond—making the subject and predicate terms line up. You do this by performing conversion, obversion, and contraposition as needed, but only when those operations produce equivalent results: you only use conversion on E and I sentences; you only use contraposition on A and O sentences; and since obversion always yields an equivalent sentence, you can use it whenever you want. Then, once you’ve achieved correspondence, you can consult the Square of Opposition and complete the inference.

Another example can help illustrate the method. Suppose we’re told that some sentence ‘All S are P’ is true. What about the sentence ‘No ~ S are ~ P’? (Remember, when we put the tildes in front of the letters, we’re referring to the complements of these classes.)

First, we notice that the subject and predicate terms don’t correspond. The A sentence has ‘S’ in subject position and ‘P’ in predicate position, while the target E sentence has ~ S and ~ P in those slots. We can see this misalignment clearly (and also set ourselves up more easily to think through the remaining steps in the inference) if we write the sentences out, one above the other (noting in brackets what we know about their truth-values):

All S are P [T]

No ~ S are ~ P [?]

Focusing only on subject and predicate terms, we see that the bottom ones have tildes, the top ones don’t. We need to get them into correspondence. How? Well, it occurs to me that we have an operation that allows us to add or remove tildes, two at a time: contraposition. When we perform that operation, we replace the subject with the complement of the predicate (adding or removing one tilde) and we replace the predicate with the complement of the subject (adding or removing another). Now, contraposition produces equivalent sentences for A and O, but not E and I. So I can only perform it on the top sentence, ‘All S are P’. Doing so, I produce a contrapositive which expresses the same proposition, and so must also be true. We can write it down like this:

All S are P	[T]
All ~ P are ~ S	[T]
No ~ S are ~ P	[?]

The sentence we just wrote down still doesn’t align with the target sentence at the bottom, but it’s closer: they both have tildes in front of ‘S’ and ‘P’. Now the problem is that the ‘~ S’ and ‘~ P’ are in the wrong order: subject and predicate positions, respectively, in the target sentence, but the reverse in the sentence we just wrote down. We have an operation to fix that! It’s called conversion: to perform it, you switch the order of subject and predicate terms. The thing is, it only works— that is, gives you an equivalent result—on E and I sentences. I can’t perform conversion on the A sentence ‘All ~ P are ~ S’ that I just wrote down at the top. But, I can perform it on the target E sentence at the bottom:

All S are P	[T]
All ~ P are ~ S	[T]
No ~ P are ~ S	[?]
No ~ S are ~ P	[?]

I did conversion, as it were, from the bottom up. Those last two E sentences are converses of one another, so they express the same proposition and will have the same truth value. If I can figure out the truth-value of ‘No ~ P are ~ S’, then I can figure out the truth-value of my target sentence on the bottom; it’ll be the same. And look! I’m finally in a position to do that. The two sentences in the middle, ‘All ~ P are ~ S’ and ‘No ~ P are ~ S’, correspond; they have the same subject and predicate. That means I can consult the Square of Opposition. I have an A sentence that’s true. What about the corresponding E sentence? They’re contraries, so it must be false:

All S are P	[T]
All ~ P are ~ S	[T]
No ~ P are ~ S	[F]
No ~ S are ~ P	[?]

And since the target sentence at the bottom expresses the same proposition as the one directly above it, that final question mark can also be replaced by an ‘F’. Inference made, problem solved.

Again, this is the general pattern for making these kinds of inferences: achieve correspondence by using the three operations, then use the information encoded in the Square of Opposition.

This works most of the time, but not always. Suppose you’re told that ‘All S are P’ is true, and asked to infer the truth-value of ‘No P are ~ S’. We can again write them out one above the other and take a look:

All S are P [T]

No P are ~ S [?]

‘S’ and ‘P’ are in the wrong order, plus ‘S’ has a tilde in front of it on the bottom but not on the top. The first thing that occurs to me to do is to get rid of that tilde. We have an operation for adding or removing one tilde at a time: obversion. I’m going to perform it on the bottom sentence. First, I change the quality: the universal negative (E) original becomes a universal affirmative (A). Then I replace the predicate with its complement: I replace ‘~ S’ with just plain ‘S’. This is the result:

All S are P [T]

All P are S [?]

No P are ~ S [?]

We don’t have correspondence yet, but we’re closer with that tilde out of the way. What next? Well, now the problem is just that ‘S’ and ‘P’ are in the wrong order. There’s an operation for that: conversion. But—and here’s the rub—we can only use conversion on E and I sentences. Now that I did obversion on the target at the bottom, the two sentences I’m left comparing are both As. I can’t use conversion on an A: the result won’t be equivalent.

At this point, the sensible thing to do would be to try other operations: maybe the right combination of obversion, contraposition, and possibly, eventually, on a different kind of sentence, conversion, will allow us to achieve correspondence. When making these kinds of inferences, you often have to try a variety of things before you get there. But I’m here to tell you, try what you might in this example, as many conversions, obversions, and contrapositions as you want, in whatever order: you’ll never achieve correspondence. It’s impossible.

So what does that mean? It means that, given the fact that ‘All S are P’ is true, you cannot make any inference about the truth-value of ‘No P are ~ S’. The answer to the problem is: “I don’t know.” Remember, this kind of thing can happen; sometimes we can’t make inferences about one categorical based on information about another. When we know that an I is true, for example, we can’t say what the truth-value of the corresponding O is; it could go either way.

That’s kind of unsatisfying, though. I’m telling you that if you can’t achieve correspondence—if it’s impossible—that you can’t make an inference. But how do you know that you can’t achieve correspondence? Maybe, as you were laboring over the problem, you just didn’t stumble on the right combination of operations in the right order. How do we know for sure that an inference can’t be made? As a matter of fact, the one step that we took in this problem puts us in a position to know just that. Compare ‘All S are P’ with the obverse of the target sentence, ‘All P are S’. What’s the relationship between those? One is the converse of the other. We’re given a true A sentence, and asked to make an inference about the truth-value of a sentence equivalent to its converse. But performing conversion on an A, as we established at length above, gives you a new sentence that expresses a different proposition. And this has unpredictable effects on truth-value: sometimes one goes from truth to falsity; other times from truth to truth, and so on. In this case, we know that we can’t know the truth-value of the target sentence, because it’s equivalent to the result of perform conversion on a universal affirmative, and the effects of that operation on truth-value are unpredictable.

In general, you can know that the answer to one of these problems is “I don’t know” if you can use the operations to get into a position where you’re comparing a sentence with its converse or contrapositive when those operations don’t work for the types of sentences you have. We saw this for an A and its converse. Similarly, if you have an E sentence of known truth-value, and your target sentence is equivalent to its contrapositive, you know the answer is “I don’t know,” because contraposition performed on E sentences has unpredictable results on truth-value. Same goes for I and conversion, O and contraposition.

EXERCISES

1. Suppose ‘All S are P’ is true. Determine the truth-values of the following (if possible).

(a) No S are ~ P

(b) All ~S are ~ P

(c) No ~ P are S

(d) Some ~ P are S

(e) Some ~ S are not ~ P

2. Suppose ‘No S are P’ is true. Determine the truth-values of the following (if possible).

(a) Some ~ P are not ~ S

(b) All ~ S are ~ P

(c) No ~ S are ~ P

(d) Some ~ P are S

(e) All ~ P are ~ S

3. Suppose ‘Some S are P’ is true. Determine the truth-values of the following (if possible).

(a) All S are ~ P

(b) Some S are not ~ P

(c) No P are S

(d) Some P are ~ S

(e) No S are ~ P

4. Suppose ‘Some S are not P’ is true. Determine the truth-values of the following (if possible).

(a) No S are ~ P

(b) Some S are ~ P

(c) No ~ S are P

(d) No ~ P are S

(e) Some P are S

V. Problems with the Square of Opposition

The Square of Opposition is an extremely useful tool: it neatly summarizes, in graphical form, everything we know about the relationships among the four types of categorical proposition.

Except, actually, we don’t know those things. I’m sorry, but when I first presented the Square of Opposition and made the case for the various relationships it depicts, I was leading you down the proverbial primrose path. What appeared easy is in fact not so simple as it seems. Some of the relationships in the Square break down under certain circumstances and force us to do some hard thinking about how to proceed. It’s time to explore the “steep and thorny way” that opens before us when we dig a bit deeper into problems that can arise for the Square of Opposition.

Existential Import

To explain what these problems are, we need the concept of existential import (E.I. for short). E.I. is a property that propositions may or may not have. A proposition has existential import when its truth implies the existence of something. Because of what we decided to mean when we use the word ‘some’—namely, ‘there is at least one’—the particular propositions I and O clearly have E.I. For ‘Some sailors are not pirates’ to be true, there has to exist at least one sailor who is not a pirate. Again, that’s just a consequence of what we mean by ‘some’.

In addition, given the relationships that are said to hold by the Square of Opposition, the universal propositions A and E also have existential import. This is because the particular propositions are subalterns. The truth of a universal proposition implies the truth of a particular one: if an A is true, then the corresponding I must be; if an E is true, then the corresponding O must be. So since the truth of universals implies the truth of particulars, and particulars have E.I., then universals imply the existence of something as well: they have existential import, too.

Problems for the Square

OK, all four of the categorical propositions have existential import. What’s the big deal? Well, this fact leads to problems. Consider the proposition that all C.H.U.D.s are Idahoans; also, consider the proposition that some C.H.U.D.s are not Idahoans. Both of these propositions are false. That’s because both of them imply the existence of things—namely, C.H.U.D.s—that don’t exist. (‘C.H.U.D.’ stands for ‘Cannibalistic Humanoid Underground Dweller’. They’re the titular scary monsters of a silly horror movie from the ’80s. They’re not real.) ‘Some C.H.U.D.s are not Idahoans’ claims that there exists at least one C.H.U.D. who’s not an Idahoan; but that’s not the case, since there are no C.H.U.D.s. ‘All C.H.U.D.s are Idahoans’ is also false: if it were true, its subaltern ‘Some C.H.U.D.s are Idahoans’ would have to be true; but it can’t be, because it claims that there’s such a thing as a C.H.U.D. (who’s an Idahoan).

Bottom line: A and O propositions about C.H.U.D.s both turn out false. This is a problem for the Square of Opposition because A and O are supposed to be a contradictory pair; they’re supposed to have opposite truth-values.

It gets worse. Any time your subject class is empty—that is, like ‘C.H.U.D.s’, it doesn’t have any members—all four of the categorical propositions turn out false. This is because, as we saw, all four have existential import. But if E and I are both false, that’s a problem: they’re supposed to be contradictory. If I and O are both false, that’s a problem: they’re supposed to be subcontraries. When we talk about empty subject classes, the relationships depicted in the Square cease to hold.

Solution?

So the problems are caused by empty classes. We can fix that. We’re building our own logic from the ground up here. Step one in that process is to tame natural language. The fact that natural language contains terms that don’t refer to anything real seems to be one of the ways in which it is unruly, in need of being tamed. Why not simply restrict ourselves to class terms that actually refer to things, rule out empty classes? Then the Square is saved.

While tempting, this solution goes too far. The fact is, we make categorical claims using empty (or at least possibly empty) class terms all the time. If we ruled these out, our ability to evaluate arguments containing such claims would be lost, and our logic would be impoverished.

One field in which logic is indispensable is mathematics. Mathematicians need precise language to prove interesting claims. But some of the most interesting claims in mathematics involve empty classes. For instance, in number theory, one can prove that there is no largest prime number—they go on forever. In other words, the term ‘largest prime number’ refers to an empty class. If our logic ruled out empty class terms, mathematicians couldn’t use it. But mathematicians are some of our best customers!

Also, physicists. Before its existence was confirmed in 2013, they made various claims about a fundamental particle called the Higgs boson. “Higgs bosons have zero spin,” they might say, making a universal affirmative claim about these particles. But before 2013, they didn’t even know if such particles existed. IF they existed, they would have zero spin (and a certain mass, etc.); the equations predicted as much. But those equations were based on assumptions that may not have been true, and so there may not have been any such particle. Nevertheless, it was completely appropriate to make claims about it, despite the fact that ‘Higgs boson’ might be an empty term.

We make universal claims in everyday life that don’t commit us to the existence of things. Consider the possible admonition of a particularly harsh military leader: Deserters will be shot. This is a universal affirmative claim. But it doesn’t commit to the existence of deserters; in fact, it’s very purpose is to ensure that the class remains empty!

So, empty classes have their uses, and we don’t want to commit ourselves to the existence of things every time we assert a universal claim. Ruling out empty classes from our logic goes too far to save the Square of Opposition. We need an alternative solution to our problems.

Boolean Solution

Advocated by the English logician George Boole in the 19^th Century, our solution to the problems raised will be to abandon the assumption that universal propositions (A and E) have existential import, allow empty classes, and accept the consequences. Those consequences, alas, are quite dire for the traditional Square of Opposition. Many of the relationships it depicts do not hold when subject classes are empty.

First, the particular propositions (I and O) are no longer subcontraries. Since they start with the word ‘some’, they have existential import. When their subject classes are empty, as is now allowed, they both turn out false. Subcontraries can’t both be false, but I and O can both be false when we allow empty classes.

Next, the particular propositions are no longer subalterns of their corresponding universals (A and E). As we said, the universals no longer have existential import—they no longer imply the existence of anything—and so their truth cannot imply the truths of particular propositions, which do continue to have E.I.

The only two relationships left on the Square now are contradictoriness—between A and O, E and I—and contrariety between the two universals. And these are in conflict when we have empty subject classes. In such cases, both I and O are false, as we’ve said. It follows that their contradictories, A and E, must be true. But, A and E are supposed to be a contrary pair; they can’t both be true. So we can’t keep both contrariety and contradictoriness; one must go. We will keep contradictoriness. To do otherwise would be to abondon the plain meanings of the words we’re using. There’s a reason I introduced this relationship first: it’s the easiest to understand. If you want to contradict my universal affirmative claim that all sailors are pirates, you claim that some of them aren’t; A and O are clearly contradictory. As are E and I: if you want to contradict my claim that no surfers are priests, you show me one who is. So we eliminate contrariety: it is possible, in cases where the subject class is empty, for both A and E propositions to be true.

What we’re left with after making these revisions is no longer a square, but an X. All that remains is contradictoriness:

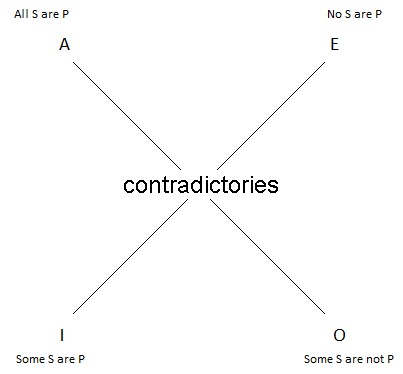
And our solution is not without awkwardness. In cases where the subject class is empty, both particular propositions (I and O) are false; their universal contradictories (E and A), then, are true in those circumstances. This is strange. Both of these sentences express truths: ‘All C.H.U.D.s are Idahoans’ and ‘No C.H.U.D.s are Idahoans’. That’s a tough pill to swallow, but swallow it we must, given the considerations above. We can make it a bit easier to swallow if we say that they’re true, but vacuously or trivially. That is, they’re true, but not in a way that tells you anything about how things actually are in the world (the world is, after all and thankfully, C.H.U.D.-free).

That we would end up choosing this interpretation of the categoricals, rather than the one under which universal propositions had existential import, was foreshadowed earlier, when we first introduced the four types of categorical proposition and talked about how to diagram them. We chose diagrams for A and E that did not imply the existence of anything. Recall that our way of indicating existence in Venn diagrams is to draw an X. So for a particular affirmative—some surfers are priests, say—we drew this picture (with the X being the one surfing priest we’re committed to the existence of):

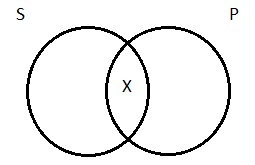
The diagrams for the universals (A and E), though, had no Xs in them, only shading; they don’t commit us to the existence of anything. If we were going to maintain the existential import of A and E, we would’ve drawn different diagrams. For the universal affirmative—all logicians are Germans, say—we’d shade out the portion of the left-hand circle that doesn’t overlap the right, to indicate that there’s no such thing as a logician who’s not a German. But we would also put an X in the middle region, to indicate that there is at least one logician who is (existential import):

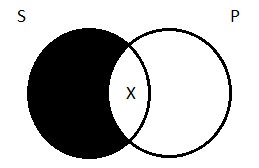
And for the universal negative—no women are priests, say—we would shade out the middle region, to indicate there’s nothing that’s both a woman and a priest. But we would also put an X in the left-hand circle, to indicate that there’s at least one woman who’s not a priest:

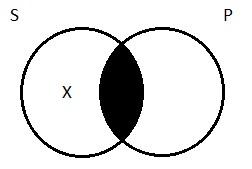
This interpretation of the universal propositions, according to which they have existential import, is often called the “Aristotelian” interpretation (as opposed to our “Boolean” interpretation, according to which they do not).^[3] Which interpretation one adopts makes a difference. There are some arguments that the two interpretations evaluate differently: on the Aristotelian view, they are valid, but on the Boolean view, they are not. We will stick to the Boolean interpretation of the universals, according to which they do not have existential import.

VI. Categorical Syllogisms

As we’ve said, Aristotelian Logic limits itself to evaluating arguments all of whose propositions— premises and conclusion—are categorical. There is a further restriction: Aristotelian Logic only evaluates categorical syllogisms. These are a special kind of argument, meeting the following conditions:

A categorical syllogism is a deductive argument consisting of three categorical propositions (two premises and a conclusion); collectively, these three propositions feature exactly three classes; each of the three classes occurs in exactly two of the propositions.

That’s a mouthful, but an example will make it clear. Here is a (silly) categorical syllogism:

All chipmunks are athletes.

Some athletes are golfers.

/∴ Some chipmunks are golfers.

This argument meets the conditions in the definition: it has three propositions; there are exactly three classes involved (chipmunks, athletes, and golfers); and each of the three classes occurs in exactly two of the propositions (check it and see).

There is some special terminology for the class terms and premises in categorical syllogisms. Each of the three class terms has a special designation. The terms in the conclusion determine the designations. The so-called major term is the term that appears in predicate position in the conclusion; in our silly example, that’s ‘golfers’. The minor term is the term that appears in subject position in the conclusion; in our example, that’s ‘chipmunks’. The middle term is the other one, the one that appears in each of the premises; in our example, it’s ‘athletes’.

The premises have special designations as well. The major premise is the one that has the major term in it; in our example, that’s ‘Some athletes are golfers’. The minor premise is the other one, the one featuring the minor term; in our example, it’s ‘All chipmunks are athletes’.

Final restriction: categorical syllogisms must be written in standard form. This means listing the premises in the correct order, with the major premise first and the minor premise second. If you look at our silly example, you’ll note that it’s not in standard form. To fix it, we need to reverse the order of the premises:

Some athletes are golfers.

All chipmunks are athletes.

/∴ Some chipmunks are golfers.

An old concern may arise again at this point: in restricting itself to such a limited class of arguments, doesn’t Aristotelian Logic run the risk of not being able to evaluate lots of real-life arguments that we care about? The response to this concern remains the same: while most (almost all) real-life arguments are not presented as standard form categorical syllogisms, a surprising number of them can be translated into that form. Arguments with more than two premises, for example, can be rewritten as chains of two-premise sub-arguments. As was the case when we raised this concern earlier, we will set aside the messy details of exactly how this is accomplished in particular cases.

Logical Form

As we said at the outset of our exploration of deductive logic, there are three things such a logic must do: (1) tame natural language; (2) precisely define logical form; and (3) develop a way to test logical forms for validity. Until now, we’ve been concerned with the first step. It’s (finally) time to proceed to the second and third.

The logical form of a categorical syllogism is determined by two features of the argument: its mood and its figure. First, mood. The mood of a syllogism is determined by the types of categorical propositions contained in the argument, and the order in which they occur. To determine the mood, put the argument into standard form, and then simply list the types of categoricals (A, E, I, O) featured in the order they occur. Let’s do this with our silly example:

Some athletes are golfers.

All chipmunks are athletes.

/∴ Some chipmunks are golfers.

From top to bottom, we have an I, an A, and an I. So the mood of our argument is IAI. It’s that easy. It turns out that there are 64 possible moods—64 ways of combining A, E, I, and O into unique three-letter combinations, from AAA to OOO and everything in between.

The other aspect of logical form is the argument’s figure. The figure of a categorical syllogism is determined by the arrangement of its terms. Given the restrictions of our definition, there are four different possibilities for standard form syllogisms. We will list them schematically, using these conventions: let ‘S’ stand for the minor term, ‘P’ stand for the major term, and ‘M’ stand for the middle term. Here are the four figures:

(1)	MP	(2)	PM	(3)	MP	(4)	PM
	SM		SM		MS		MS
	∴ SP		∴ SP		∴ SP		∴ SP

Again, the only thing that determines figure is the arrangement of terms—whether they appear in subject or predicate position in their premises. In our schemata, that the letter is listed first indicates that the term appears in subject position; that it appears second indicates that it’s in predicate position. So, in the first figure, in the major premise (the first one), the middle term (M) is in subject position and the major term (P) is in predicate position. Notice that for all four figures, the subject and predicate of the conclusion remains the same: this is because, by definition, the minor term (S) is the subject of the conclusion and the major term (P) its predicate.

Returning to our silly example, we can determine its figure:

Some athletes are golfers.

All chipmunks are athletes.

/∴ Some chipmunks are golfers.

Perhaps the easiest thing to do is focus on the middle term, the one that appears in each of the premises—in this case, ‘athletes’. It occurs in subject position in the major premise, then predicate position in the minor premise. Scanning the four figures, I just look for the one that has ‘M’ listed in first position on the top, then second position in the middle. That’s the first figure.

So the mood of our sample argument is IAI, and it’s in the first figure. Logical form is just the mood and figure, and conventionally, we list logical forms like this: IAI-1 (the mood, a dash, then a number between 1 and 4 for the figure).

There are 4 figures and 64 moods. That gives us 256 possible logical forms. It turns out that only 15 of these are valid. We need a way to test them. It is to that task we now turn.

The Venn Diagram Test for Validity

To test syllogistic forms for validity, we proceed in three steps:

Draw three overlapping circles, like this:

 

That gives us one circle for each of the three terms in the syllogism: minor (S), major (P), and middle (M). It is useful to write out your argument in standard form. Label the subject and predicate in the conclusion with S and P. Then match those labels to the other places those words appear in the premises. Write an M above the middle term shared by both premises.

Depict the assertions made by the premises of the syllogism on this diagram, using shading and Xs as appropriate, depicting the individual A, E, I, or O propositions in the usual way. For the sake of clarity, only the two relevant circles to any given premise are shown below – your Venn would have a third circle hanging out.

 

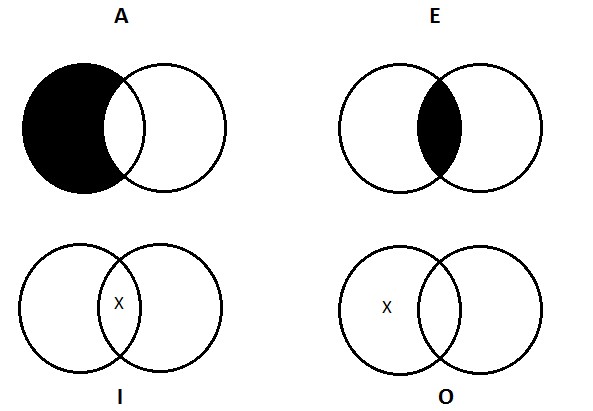
Each of the premises will be a proposition concerning only two of the three classes (S, P, and M). The major premise will concern M and P (in some order); the minor premise will concern M and S (in some order). How the circles will be labeled (with S, M, P) will depend on these particulars.

After the premises have been depicted on the three-circle diagram, we look at the finished product and ask, “Does this picture entail the truth of the conclusion?” If it does, the form is valid; if it does not, it is invalid.

In the course of running the test, we will keep two things in mind—one rule of thumb and one convention:

Rule of Thumb: If you can, go big first! In step 2, if a premise is an A or and E, start with that one. Depicting universal (A and E) premises before particular (I and O) ones (if there’s a choice) will help things go smoothly.

Convention: In cases of indeterminacy, draw Xs straddling boundary lines.

We need to explain what “indeterminacy” amounts to; we will in a moment. For now, to make all this more clear, we should run through some examples.

Let’s start at the beginning (alpha-numerically): AAA-1. We want to test this syllogistic form for validity. What does an argument of this form look like, schematically? Well, all three of its propositions are universal affirmatives, so they’re all of the form All __ are __. We have:

All __ are __

All __ are __

/∴ All __ are __

That’s what the mood (AAA) tells us. We have to figure out how to fill in the blanks with S, P, and M. The figure tells us how to do that. AAA-1: so, first figure. That looks like this:

(i) MP

    SM

  ∴ SP

So AAA-1 can be schematically rendered thus:

All M are P.

All S are M.

/∴ All S are P.

To test this form for validity, we start with step 1, and draw three circles:

In step 2, we depict the premises on this diagram. (We’re supposed to keep in mind the rule of thumb that, given a choice, we should depict universal premises before particular ones, but since both of the premises are universals, this rule does not apply to this case.) We can start with the major premise: All M are P. On a regular two-circle Venn diagram, that would look like this:

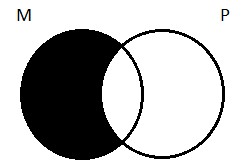
The trick is to transfer this two-circle diagram onto the three-circle one. In doing so, we keep in mind that all the parts of M that are outside of P must be shaded. That gives us this:

Note that in the course of shading out the necessary regions of M, we shaded out part of S. That’s OK. Those members of the S class are Ms that aren’t Ps; there’s no such thing, so they have to go.

Next, we depict the minor premise: All S are M. With two circles, that would look like this:

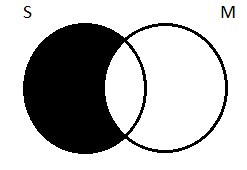
Transferring that onto the three circle diagram means shading all the parts of S outside of M:

Step 2 is complete: we have depicted the assertions made by the premises. In step 3 we ask whether this diagram guarantees the truth of the conclusion. Well, our conclusion is All S are P. In a two-circle diagram, that looks like this:

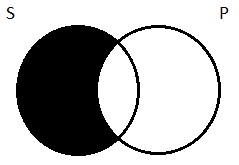
Does our three-circle diagram guarantee the truth of All S are P? Focusing on the S and P circles, and comparing the two diagrams, there’s a bit of a difference: part of the area of overlap between S and P is shaded out in our three-circle diagram, but it isn’t in the two-circle depiction. But that doesn’t affect our judgment about whether the diagram guarantees All S are P. Remember, this can be thought of as a claim that a certain kind of thing doesn’t exist—an S that’s outside the P circle.If there are any Ss (and there may not be), they will also be Ps. Our three-circle diagram does in fact guarantee this. There can’t be an S that’s not a P; those areas are shaded out. Any S you find will also be a P; it’ll be in that little region in the center where all three circles overlap.

So, since the answer to our question is “yes”, the syllogistic form AAA-1 is valid. Trivial fact: all the valid syllogistic forms were given mnemonic nicknames in the Middle Ages to help students remember them. AAA-1 is called “Barbara”. No really. All the letters in the name had some meaning: the vowels indicate the mood (AAA); the other letters stand for features of the form that go beyond our brief investigation into Aristotelian Logic.

We should reflect for a moment on why this method works. We draw a picture that depicts the assertions made by the premises of the argument. Then we ask whether that picture guarantees the conclusion. This should sound familiar. We’re testing for validity, and by definition, an argument is valid just in case its premises guarantee its conclusion; that is, IF the premises are true, then the conclusion must also be true. Our method mirrors the definition. When we depict the premises on the three-circle diagram, we’re drawing a picture of what it looks like for the premises to be true. Then we ask, about this picture—which shows a world in which the premises are true—whether it forces us to accept the conclusion—whether it depicts a world in which the conclusion must be true. If it does, the argument is valid; if it doesn’t, then it isn’t. The method follows directly from the definition of validity.

To further illustrate the method, we should do some more examples. AII-3 is a useful one. The mood tells us it’s going to look like this:

All __ are __

Some __ are __

/∴ Some __ are __

And we’re in the third figure:

(iii) MP

       MS

       SP

So we fill in the blanks to get the schematic form:

All M are P

Some M are S

/∴ Some S are P

We start the test of this form with the blank three-circle diagram:

Step 2: depict the premises. And here, our rule of thumb applies: depict universals before particulars. The major premise is a universal (A) proposition; the minor premise is a particular (I). So we depict the major premise first. That’s All M are P. We did this already. Recall that Barbara has the same major premise. So depicting that on the diagram gives us this:

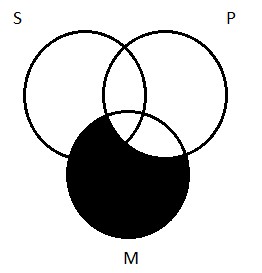
Next, the minor premise: Some M are S. Recall, with particular propositions, we depict them using an X to indicate the thing said to exist. This proposition asserts that there is at least one thing that is both M and S:

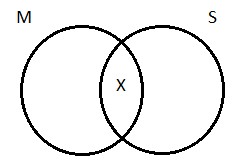
We need to transfer this to the three-circle diagram. We need an X that is in both the M and S circles. If we look at the area of overlap between the two, we see that part of it has been shaded out as the result of depicting the major premise, so there’s only one place for the X to go:

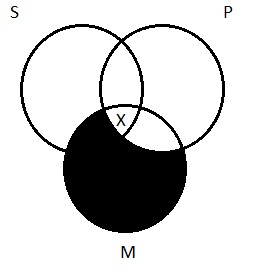
Step 2 is complete: the premises are depicted. So we proceed to step 3 and ask, “Does this picture guarantee the conclusion?” The conclusion is Some S are P; that’s an assertion that there is at least one thing that is both S and P. Is there? Yes! That X that we drew in the course of depicting the minor premise is in the sweet spot—the area of overlap between S and P. It guarantees the conclusion. The argument is valid. (If you’re curious, its mnemonic nickname is ‘Datisi’. Weird, I know; it was the Middle Ages.)

That’s another successful use of the Venn diagram test for validity, but I want to go back a revisit some of it. I want us to reflect on why we have the rule of thumb to depict universal premises before particular ones. Remember, we had the universal major premise All M are P and the particular minor premise Some M are S. The rule of thumb had us depict them in that order. Why? What would have happened had we done things the other way around? We would have started with a blank three-circle diagram and had to depict Some M are S on it. That means an X in the area of overlap between M and S. That area, though, is divided into two sub-regions (labeled ‘a’ and ‘b’):

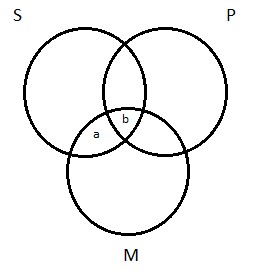
Where do I put my X—in region a or b? Notice, it makes a difference: if I put the X is region a, then it’s outside the P circle; if I put it in region b, then it’s inside the P circle. The question is: “Is this thing that the minor premise says exists a P or not a P?” I’m depicting a premise that only asserts Some M are S. That premise says nothing about P. It’s silent on our question; it gives us no guidance about how to choose between regions a and b. What to do? This is one of the cases of “indeterminacy” that we mentioned earlier when we introduced a convention to keep in mind when running the test for validity: In cases of indeterminacy, draw Xs straddling boundary lines. We don’t have any way of choosing between regions a and b, so when we draw our X, we split the difference:

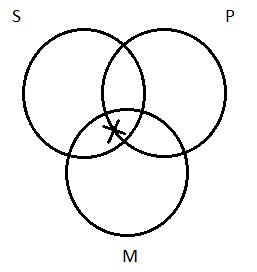
This drawing indicates that there’s an X in there somewhere, either inside or outside the P circle, we don’t know which.

And now we see the reason for our rule of thumb—depict universals before particulars. Because if we proceed to depict the universal premise All M are P, we shade thus:

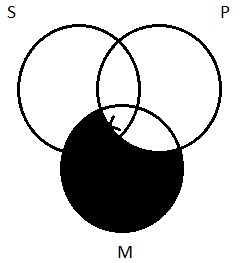
The shading erased half our X. That is, it resolved our question of whether or not the X should go in the P circle: it should. So now we have to go back an erase the half-an-X that’s left and re-draw the X in that center region and end up with the finished diagram we arrived at earlier:

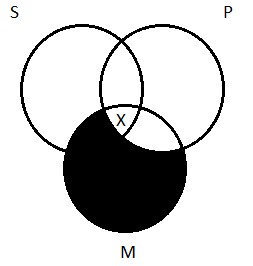
We would’ve saved ourselves the trouble had we just followed the rule of thumb to begin with and depicted the universal before the particular—shading before the X. That’s the utility of the rule: sometimes it removes indeterminacy that would otherwise be present.

One more example to illustrate how this method works. Let’s test EOI-1. Noting that in the first figure the middle term is first subject and then predicate, we can quickly fill in the schema:

No M are P

Some S are not M.

/∴ Some S are P.

Following the rule of thumb, we depict the universal (E) premise first. No M are P asserts that there is nothing that is in both of those classes. The area of overlap between them is empty. With two circles, we have this:

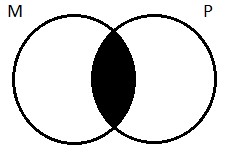
Transferring this onto the three-circle diagram, we shade out all the area of overlap between the M and P circles (clipping off part of S along the way):

Next, the particular (O) premise: Some S are not M. This asserts the existence of something— namely, a thing that is an S but not an M. We need an X in the S circle that outside the M circle:

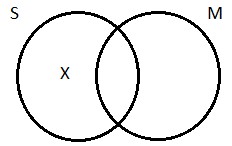
Moving to the three-circle diagram, though, things get messy. The area of S that’s outside of M is divided into two sub-regions (labeled ‘a’ and ‘b’):

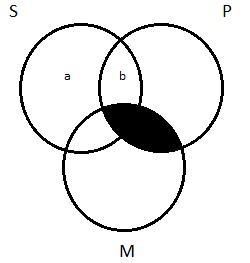
We need an X somewhere in there, but do we put it in region a or region b? It makes a difference: if we put it in region b, it is a P; if we put it in region a, it is not. This is the same problem we faced before. We’re depicting a premise—Some S are not M—that is silent on the question of whether or not the thing is a P. Indeterminacy. We can’t decide between a and b, so we split the difference:

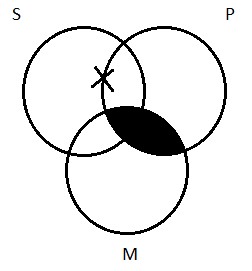
That X may be inside of P, or it may not; we don’t know. This is a case in which we followed the rule of thumb, depicting the universal premise before the particular one, but it didn’t have the benefit that it had when we tested AII-3: it didn’t remove indeterminacy. That can happen. The rule of thumb is in place because it sometimes removes indeterminacy; it doesn’t always work, though.

So now that we’ve depicted the premises, we ask whether they guarantee the conclusion. Is the world depicted in our diagram one in which the conclusion must be true? The conclusion is Some S are P: it asserts that there is at least one thing that is both S and P. Does our picture have such a thing? There’s an X in the picture. Does it fit the bill? Is it both S and P? Well, uh… Maybe? That X may be inside of the area of overlap between S and P; then again, it may not be.

Oy. What do we say? It’s tempting to say this: we don’t know whether the argument is valid or not; it depends on where that X really is. But that’s not the correct response. Remember, we’re testing for validity—for whether or not the premises guarantee the conclusion. We can answer that question: they don’t. For a guarantee, we would need an X in our picture that is definitely inside that middle region. We don’t have such an X. These premises leave open the possibility that the conclusion is true; they don’t rule it out. But that’s not enough for validity. For an argument to be valid, the premises must necessitate the conclusion, force it on us. These do not. The form EOI1 is not valid.

EXERCISES

1. Identify the logical form of the following arguments.

(a) Because some Wisconsinites are criminals and all criminals are scoundrels, it follows that some scoundrels are Wisconsinites.

(b) No surfers are priests, because all priests are men and some surfers are not men.

(c) Some authors are feminists, since some women are authors and some women are feminists.

(d) All mosquitoes are potential carriers of disease; therefore some mosquitoes are a menace to society, since all potential carriers of disease are a menace to society.

(e) Because some neo-Nazis are bloggers, some neo-Nazis are not geniuses, since no geniuses are bloggers.

2. Test the following syllogistic forms for validity.

(a) EAE-2

(b) EAE-3

(c) OAO-3

(d) EIO-4

(e) AOO-4

(f) IAI-1

(g) AII-1

3. Test the following arguments for validity.

(a) Some pirates are mercenaries; hence, some sailors are pirates, because all sailors are mercenaries.

(b) Some women are not nuns, but all nuns are sweethearts; it follows that some women are not sweethearts.

(c) Some forks are not utensils, for some forks are not cutlery, and some cutlery are not utensils.

4. Test the arguments in Exercise 1 for validity.