8
Matthew Knachel
Inductive Logic II: Probability and Statistics
I. The Probability Calculus
Inductive arguments, recall, are arguments whose premises support their conclusions insofar as they make them more probable. The more probable the conclusion in light of the premises, the stronger the argument; the less probable, the weaker. As we saw in the last chapter, it is often impossible to say with any precision exactly how probable the conclusion of a given inductive argument is in light of its premises; often, we can only make relative judgments, noting that one argument is stronger than another, because the conclusion is more probable, without being able to specify just how much more probable it is.
Sometimes, however, it is possible to specify precisely how probable the conclusion of an inductive argument is in light of its premises. To do that, we must learn something about how to calculate probabilities; we must learn the basics of the probability calculus. This is the branch of mathematics dealing with probability computations.[1] We will cover its most fundamental rules and learn to perform simple calculations. After that preliminary work, we use the tools provided by the probability calculus to think about how to make decisions in the face of uncertainty, and how to adjust our beliefs in the light of evidence. We will consider the question of what it means to be rational when engaging in these kinds of reasoning activities.
Finally, we will turn to an examination of inductive arguments involving statistics. Such arguments are of course pervasive in public discourse. Building on what we learned about probabilities, we will cover some of the most fundamental statistical concepts. This will allow us to understand various forms of statistical reasoning—from different methods of hypothesis testing to sampling techniques. In addition, even a rudimentary understanding of basic statistical concepts and reasoning methods will put us in a good position to recognize the myriad ways in which statistics are misunderstood, misused, and deployed with the intent to manipulate and deceive. As Mark Twain said, “There are three kinds of lies: lies, damned lies, and statistics.”[2] Advertisers, politicians, pundits—everybody in the persuasion business—trot out statistical claims to bolster their arguments, and more often than not they are either deliberately or mistakenly committing some sort of fallacy. We will end with a survey of these sorts of errors.
But first, we examine the probability calculus. Our study of how to compute probabilities will divide neatly into two sections, corresponding to the two basic types of probability calculations one can make. There are, on the one hand, probabilities of multiple events all occurring—or, equivalently, multiple propositions all being true; call these conjunctive occurrences. We will first learn how to calculate the probabilities of conjunctive occurrences—that this event and this other event and some other event and so on will occur. On the other hand, there are probabilities that at least one of a set of alternative events will occur—or, equivalently, that at least one of a set of propositions will be true; call these disjunctive occurrences. In the second half of our examination of the probability calculus we will learn how to calculate the probabilities of disjoint occurrences— that this event or this other event or some other event or… will occur.
Conjunctive Occurrences
Recall from our study of sentential logic that conjunctions are, roughly, ‘and’-sentences. We can think of calculating the probability of conjunctive occurrences as calculating the probability that a particular conjunction is true. If you roll two dice and want to know your chances of getting “snake eyes” (a pair of ones), you’re looking for the probability that you’ll get a one on the first die and a one on the second.
Such calculations can be simple or slightly more complex. What distinguishes the two cases is whether or not the events involved are independent. Events are independent when the occurrence of one has no effect on the probability that any of the others will occur. Consider the dice mentioned above. We considered two events: one on die #1, and one on die #2. Those events are independent. If I get a one on die #1, that doesn’t affect my chances of getting a one on the second die; there’s no mysterious interaction between the two dice, such that what happens with one can affect what happens with the other. They’re independent.[3] On the other hand, consider picking two cards from a standard deck (and keeping them after they’re drawn).[4] Here are two events: the first card is a heart, the second card is a heart. Those events are not independent. Getting a heart on the first draw affects your chances of getting a second heart (it makes the second heart less likely).
When events are independent, things are simple. We calculate the probability of their conjunctive occurrence by multiplying the probabilities of their individual occurrences. This is the Simple Product Rule:
P(a • b • c • …) = P(a) x P(b) x P(c) x …
This rule is abstract; it covers all cases of the conjunctive occurrence of independent events. ‘a’, ‘b’, and ‘c’ refer to events; the ellipses indicate that there may be any number of them. When we write ‘P’ followed by something in parentheses, that’s just the probability of the thing in parentheses coming to pass. On the left-hand side of the equation, we have a bunch of events with dots in between them. The dot means the same thing it did in SL: it’s short for and. So this equation just tells us that to compute the probability of a and b and c (and however many others there are) occurring, we just multiply together the individual probabilities of those events occurring on their own.
Go back to the dice above. We roll two dice. What’s the probability of getting a pair of ones? The events—one on die #1, one on die #2—are independent, so we can use the Simple Product Rule and just multiply together their individual probabilities.
What are those probabilities? We express probabilities as numbers between 0 and 1. An event with a probability of 0 definitely won’t happen (a proposition with a probability of 0 is certainly false); an event with a probability of 1 definitely will happen (a proposition with a probability of 1 is certainly true). Everything else is a number in between: closer to 1 is more probable; closer to 0, less. So, how probable is it for a rolled die to show a one? There are six possible outcomes when you roll a die; each one is equally likely. When that’s the case, the probability of the particular outcome is just 1 divided by the number of possibilities. The probability of rolling a one is 1/6.
So, we calculate the probability of rolling “snake eyes” as follows:
P(one on die #1 • one on die #2) = P(one on die #1) x P(one on die #2)
= 1/6 x 1/6
= .0278
If you roll two dice a whole bunch of times, you’ll get a pair of one a little less than 3% of the time.
We noted earlier that if you draw two cards from a deck, two possible outcomes—first card is a heart, second card is a heart —are not independent. So we couldn’t calculate the probability of getting two spades using the Simple Product Rule. We could only do that if we made the two events independent—if we stipulated that after drawing the first card, you put it (randomly) back into the deck, so you’re picking at random from a full deck of cards each time. In that case, you’ve got a 1/4 chance of picking a heart each time, so the probability of picking two in a row would be 1/4 x 1/4—and the probability of picking three in a row would be 1/4 x 1/4 x 1/4, and so on.
Of course the more interesting question—and the more practical one, if you’re a card player looking for an edge—is the original one: what’s the probability of, say, drawing three hearts assuming, as is the case in all real-life card games, that you keep the cards as you draw them? As we noted, these events— heart on the first card, heart on the second card, heart on the third card— are not independent, because each time you succeed in drawing a heart, that affects your chances (negatively) of drawing another one. Let’s think about this effect in the current case. The probability of drawing the first heart from a well-shuffled, complete deck is simple: 1/4. It’s the subsequent hearts that are complicated. How much of an effect does success at drawing that first heart have on the probability of drawing the second one? Well, if we’ve already drawn one heart, the deck from which we’re attempting to draw the second is different from the original, full deck: specifically, it’s short the one card already drawn—so there are only 51 total—and it’s got fewer hearts now—12 instead of the original 13. 12 out of the remaining 51 cards are hearts, then. So the probability of drawing a second heart, assuming the first one has already been picked, is 12/51. If we succeed in drawing the second heart, what are our chances at drawing a third? Again, in this case, the deck is different: we’re now down to 50 total cards, only 11 of which are hearts. So the probability of getting the third heart is 11/50.
It’s these fractions—1/4, 12/51, and 11/50—that we must multiply together to determine the probability of drawing three straight hearts while keeping the cards. The result is (approximately) .013—a lower probability than that of picking 3 straight hearts when the cards are not kept, but replaced after each selection: 1/4 x 1/4 x 1/4 = .016 (approximately). This is as it should be: it’s harder to draw three straight hearts when the cards are kept, because each success diminishes the probability of drawing another heart. The events are not independent.
In general, when events are not independent, we have to make the same move that we made in the three-hearts case. Rather than considering the stand-alone probability of a second and third heart— as we could in the case where the events were independent—we had to consider the probability of those events assuming that other events had already occurred. We had to ask what the probability was of drawing a second heart, given that the first one had already been drawn; then we asked after the probability of drawing the third heart, given that the first two had been drawn.
We call such probabilities—the likelihood of an event occurring assuming that others have occurred—conditional probabilities. When events are not independent, the Simple Product Rule does not apply; instead, we must use the General Product Rule:
P(a • b • c • …) = P(a) x P(b | a) x P(c | a • b) x …
The term ‘P(b | a)’ stands for the conditional probability of b occurring, provided a already has. The term ‘P(c | a • b)’ stands for the conditional probability of c occurring, provided a and b already have. If there were a fourth event, d, we would have a this term on the right-hand side of the equation: ‘P(d | a • b • c)’. And so on.
Let’s reinforce our understanding of how to compute the probabilities of conjunctive occurrences with a sample problem:
There is an urn filled with marbles of various colors. Specifically, it contains 20 red marbles, 30 blue marbles, and 50 white marbles. If we select 4 marbles from the earn at random, what’s the probability that all four will be blue, (a) if we replace each marble after drawing it, and (b) if we keep each marble after drawing it?
Let’s let ‘B1’ stand for the event of picking a blue marble on the first selection; and we’ll let ‘B2’, ‘B3’, and ‘B4’ stand for the events of picking blue on the second, third, and fourth selections, respectively. We want the probability of all of these events occurring:
P(B1 • B2 • B3 • B4) = ?
If we replace each marble after drawing it, then the events are independent: selecting blue on one drawing doesn’t affect our chances of selecting blue on any other; for each selection, the urn has the same composition of marbles. Since the events are independent in this case, we can use the Simple Product Rule to calculate the probability:
P(B1 • B2 • B3 • B4) = P(B1) x P(B2) x P(B3) x P(B4)
And since there are 100 total marbles in the urn, and 30 of them are blue, on each selection we have a 30/100 (= .3) probability of picking a blue marble.
P(B1 • B2 • B3 • B4) = .3 x .3 x .3 x .3 = .0081
If we don’t replace the marbles after drawing them, then the events are not independent: each successful selection of a blue marble affects our chances (negatively) of drawing another blue marble. When events are not independent, we need to use the General Product Rule:
P(B1 • B2 • B3 • B4) = P(B1) x P(B2 | B1) x P(B3 | B1 • B2) x P(B4 | B1 • B2 • B3)
On the first selection, we have the full urn, so P(B1) = 30/100. But for the second term in our product, we have the conditional probability P(B2 | B1); we want to know the chances of selecting a second blue marble on the assumption that the first one has already been selected. In that situation, there are only 99 total marbles left, and 29 of them are blue. For the third term in our product, we have the conditional probability P(B3 | B1 • B2); we want to know the chances of drawing a third blue marble on the assumption that the first and second ones have been selected. In that situation, there are only 98 total marbles left, and 28 of them are blue. And for the final term—P(B4 | B1 • B2 • B3)—we want the probability of a fourth blue marble, assuming three have already been picked; there are 27 left out of a total of 97.
P(B1 • B2 • B3 • B4) = 30/100 x 29/99 x 28/98 x 27/97 = .007 (approximately)
Disjunctive Occurrences
Conjunctions are (roughly) ‘and’-sentences. Disjunctions are (roughly) ‘or’-sentences. So we can think of calculating the probability of disjunctive occurrences as calculating the probability that a particular disjunction is true. If, for example, you roll a die and you want to know the probability that it will come up with an odd number showing, you’re looking for the probability that you’ll roll a one or you’ll roll a three or you’ll roll a five.
As was the case with conjunctive occurrences, such calculations can be simple or slightly more complex. What distinguishes the two cases is whether or not the events involved are mutually exclusive. Events are mutually exclusive when at most one of them can occur—when the occurrence of one precludes the occurrence of any of the others. Consider the die mentioned above. We considered three events: it comes up showing one, it comes up showing three, and it comes up showing five. Those events are mutually exclusive; at most one of them can occur. If I roll a one, that means I can’t roll a three or a five; if I roll a three, that means I can’t roll a one or a five; and so on. (At most one of them can occur; notice, it’s possible that none of them occur.) On the other hand, consider the dice example from earlier: rolling two dice, with the events under consideration rolling a one on die #1 and rolling a one on die #2. These events are not mutually exclusive. It’s not the case that at most one of them could happen; they could both happen—we could roll snake eyes.
When events are mutually exclusive, things are simple. We calculate the probability of their disjunctive occurrence by adding the probabilities of their individual occurrences. This is the Simple Addition Rule:
P(a ∨ b ∨ c ∨ …) = P(a) + P(b) + P(c) + …
This rule exactly parallels the Simple Product Rule from above. We replace that rule’s dots with wedges, to reflect the fact that we’re calculating the probability of disjunctive rather than conjunctive occurrences. And we replace the multiplication signs with additions signs on the righthand side of the equation to reflect the fact that in such cases we add rather than multiply the individual probabilities.
Go back to the die above. We roll it, and we want to know the probability of getting an odd number. There are three mutually exclusive events—rolling a one, rolling a three, and rolling a five—and we want their disjunctive probability; that’s P(one ∨ three ∨ five). Each individual event has a probability of 1/6, so we calculate the disjunctive occurrence with the Simple Addition Rule thus:
P(one ∨ three ∨ five) = P(one) + P(three) + P(five)
= 1/6 + 1/6 + 1/6 = 3/6 = 1/2
This is a fine result, because it’s the result we knew was coming. Think about it: we wanted to know the probability of rolling an odd number; half of the numbers are odd, and half are even; so the answer better be 1/2. And it is.
Now, when events are not mutually exclusive, the Simple Addition Rule cannot be used; its results lead us astray. Consider a very simple example: flip a coin twice; what’s the probability that you’ll get heads at least once? That’s a disjunctive occurrence: we’re looking for the probability that you’ll get heads on the first toss or heads on the second toss. But these two events—heads on toss #1, heads on toss #2—are not mutually exclusive. It’s not the case that at most one can occur; you could get heads on both tosses. So in this case, the Simple Addition Rule will give us screwy results. The probability of tossing heads is 1/2, so we get this:
P(heads on #1 ∨ heads on #2) = P(heads on #1) + P(heads on #2)
= 1/2 + 1/2 = 1 [WRONG!]
If we use the Simple Addition Rule in this case, we get the result that the probability of throwing heads at least once is 1; that is, it’s absolutely certain to occur. Talk about screwy! We’re not guaranteed to gets heads at least once; we could toss tails twice in a row.
In cases such as this, where we want to calculate the probability of the disjunctive occurrence of events that are not mutually exclusive, we must do so indirectly, using the following universal truth:
P(success) = 1 – P(failure)
This formula holds for any event or combination of events whatsoever. It says that the probability of any occurrence (singular, conjunctive, disjunctive, whatever) is equal to 1 minus the probability that it does not occur. ‘Success’ = it happens; ‘failure’ = it doesn’t. Here’s how we arrive at the formula. For any occurrence, there are two possibilities: either it will come to pass or it will not; success or failure. It’s absolutely certain that at least one of these two will happen; that is, P(success failure) = 1. Success and failure are (obviously) mutually exclusive outcomes (they can’t both happen). So we can express P(success failure) using the Simple Addition Rule: P(success failure) = P(success) + P(failure). And as we’ve already noted, P(success failure) = 1, so P(success) + P(failure) = 1. Subtracting P(failure) from each side of the equation gives us our universal formula: P(success) = 1 – P(failure).
Let’s see how this formula works in practice. We’ll go back to the case of flipping a coin twice. What’s the probability of getting at least one head? Well, the probability of succeeding in getting at least one head is just 1 minus the probability of failing. What does failure look like in this case? No heads; two tails in a row. That is, tails on the first toss and tails on the second toss. See that ‘and’ in there? (I italicized it.) This was originally a disjunctive-occurrence calculation; now we’ve got a conjunctive occurrence calculation. We’re looking for the probability of tails on the first toss and tails on the second toss:
P(tails on toss #1 • tails on toss #2) = ?
We know how to do problems like this. For conjunctive occurrences, we need first to ask whether the events are independent. In this case, they clearly are. Getting tails on the first toss doesn’t affect my chances of getting tails on the second. That means we can use the Simple Product Rule:
P(tails on toss #1 • tails on toss #2) = P(tails on toss #1) x P(tails on toss #2)
= 1/2 x 1/2 = 1/4
Back to our universally true formula: P(success) = 1 – P(failure). The probability of failing to toss at least one head is 1/4. The probability of succeeding in throwing at least one head, then, is just 1 – 1/4 = 3/4.[5]
So, generally speaking, when we’re calculating the probability of disjunctive occurrences and the events are not mutually exclusive, we need to do so indirectly, by calculating the probability of the failure of any of the disjunctive occurrences to come to pass and subtracting that from 1. This has the effect of turning a disjunctive occurrence calculation into a conjunctive occurrence calculation: the failure of a disjunction is a conjunction of failures. This is a familiar point from our study of SL in Chapter 4. Failure of a disjunction is a negated disjunction; negated disjunctions are equivalent to conjunctions of negations. This is one of DeMorgan’s Theorems:
~ (p ∨ q) ≡ ~ p • ~ q
Let’s reinforce our understanding of how to compute probabilities with another sample problem. This problem will involve both conjunctive and disjunctive occurrences.
There is an urn filled with marbles of various colors. Specifically, it contains 20 red marbles, 30 blue marbles, and 50 white marbles. If we select 4 marbles from the urn at random, what’s the probability that all four will be the same color, (a) if we replace each marble after drawing it, and (b) if we keep each marble after drawing it? Also, what’s the probability that at least one of our four selections will be red, (c) if we replace each marble after drawing it, and (d) if we keep each marble after drawing it?
This problem splits into two: on the one hand, in (a) and (b), we’re looking for the probability of drawing four marbles of the same color; on the other hand, in (c) and (d), we want the probability that at least one of the four will be red. We’ll take these two questions up in turn.
First, the probability that all four will be the same color. We dealt with a narrower version of this question earlier when we calculated the probability that all four selections would be blue. But the present question is broader: we want to know the probability that they’ll all be the same color, not just one color (like blue) in particular, but any of the three possibilities—red, white, or blue. There are three ways we could succeed in selecting four marbles of the same color: all four red, all four white, or all four blue. We want the probability that one of these will happen, and that’s a disjunctive occurrence:
P(all 4 red ∨ all 4 white ∨ all 4 blue) = ?
When we are calculating the probability of disjunctive occurrences, our first step is to ask whether the events involved are mutually exclusive. In this case, they clearly are. At most, one of the three events—all four red, all four white, all four blue—will happen (and probably none of them will); we can’t draw four marbles and have them all be red and all be white, for example. Since the events are mutually exclusive, we can use the Simple Addition Rule to calculate the probability of their disjunctive occurrence:
P(all 4 red ∨ all 4 white ∨ all 4 blue) = P(all 4 red) + P(all 4 white) + P(all 4 blue)
So we need to calculate the probabilities for each individual color—that all will be red, all white, and all blue—and add those together. Again, this is the kind of calculation we did earlier, in our first practice problem, when we calculated the probability of all four marbles being blue. We just have to do the same for red and white. These are calculations of the probabilities of conjunctive occurrences:
P(R1 • R2 • R3 • R4) = ?
P(W1 • W2 • W3 • W4) = ?
(a) If we replace the marbles after drawing them, the events are independent, and so we can use the Simple Product Rule to do our calculations:
P(R1 • R2 • R3 • R4) = P(R1) x P(R2) x P(R3) x P(R4)
P(W1 • W2 • W3 • W4) = P(W1) x P(W2) x P(W3) x P(W4)
Since 20 of the 100 marbles are red, the probability of each of the individual red selections is .2; since 50 of the marbles are white, the probability for each white selection is .5.
P(R1 • R2 • R3 • R4) = .2 x .2 x .2 x .2 = .0016
P(W1 • W2 • W3 • W4) = .5 x .5 x .5 x .5 = .0625
In our earlier sample problem, we calculated the probability of picking four blue marbles: .0081. Putting these together, the probability of picking four marbles of the same color:
P(all 4 red ∨ all 4 white ∨ all 4 blue) = P(all 4 red) + P(all 4 white) + P(all 4 blue)
= .0016 + .0625 + .0081
= .0722
(b) If we don’t replace the marbles after each selection, the events are not independent, and so we must use the General Product Rule to do our calculations. The probability of selecting four red marbles is this:
P(R1 • R2 • R3 • R4) = P(R1) x P(R2 | R1) x P(R3 | R1 • R2) x P(R4 | R1 • R2 • R3)
We start with 20 out of 100 red marbles, so P(R1) = 20/100. On the second selection, we’re assuming the first red marble has been drawn already, so there are only 19 red marbles left out of a total of 99; P(R2 | R1) = 19/99. For the third selection, assuming that two red marbles have been drawn, we have P(R3 | R1 • R2) = 18/98. And on the fourth selection, we have P(R4 | R1 • R2 • R3) = 17/97.
P(R1 • R2 • R3 • R4) = 20/100 x 19/99 x 18/98 x 17/97 = .0012 (approximately)
The same considerations apply to our calculation of drawing four white marbles, except that we start with 50 of those on the first draw:
P(W1 • W2 • W3 • W4) = 50/100 x 49/99 x 48/98 x 47/97 = .0587 (approximately)
In our earlier sample problem, we calculated the probability of picking four blue marbles as .007. Putting these together, the probability of picking four marbles of the same color:
P(all 4 red ∨ all 4 white ∨ all 4 blue) = P(all 4 red) + P(all 4 white) + P(all 4 blue)
= .0012 + .0587 + .007
= .0669 (approximately)
As we would expect, there’s a slightly lower probability of selecting four marbles of the same color when we don’t replace them after each selection.
We turn now to the second half of the problem, in which we are asked to calculate the probability that at least one of the four marbles selected will be red. The phrase ‘at least one’ is a clue: this is a disjunctive occurrence problem. We want to know the probability that the first marble will be red or the second will be red or the third or the fourth:
P(R1 ∨ R2 ∨ R3 ∨ R4) = ?
When our task is to calculate the probability of disjunctive occurrences, the first step is to ask whether the events are mutually exclusive. In this case, they are not. It’s not the case that at most one of our selections will be a red marble; we could pick two or three or even four (we calculated the probability of picking four just a minute ago). That means that we can’t use the Simple Addition Rule to make this calculation. Instead, we must calculate the probability indirectly, relying on the fact that P(success) = 1 – P(failure). We must subtract the probability that we don’t select any red marbles from 1:
P(R1 ∨ R2 ∨ R3 ∨ R4) = 1 – P(no red marbles)
As is always the case, the failure of a disjunctive occurrence is just a conjunction of individual failures. Not getting any red marbles is failing to get a red marble on the first draw and failing to get one on the second draw and failing on the third and on the fourth:
P(R1 ∨ R2 ∨ R3 ∨ R4) = 1 – P(~ R1 • ~ R2 • ~ R3 • ~ R4)
In this formulation, ‘~ R1’ stands for the eventuality of not drawing a red marble on the first selection, and the other terms for not getting red on the subsequent selections. Again, we’re just borrowing symbols from SL.
Now we’ve got a conjunctive occurrence problem to solve, and so the question to ask is whether the events ~ R1, ~ R2, and so on are independent or not. And the answer is that it depends on whether we replace the marbles after drawing them or not.
If we replace the marbles after each selection, then failure to pick red on one selection has no effect on the probability of failing to select red subsequently. It’s the same urn— with 20 red marbles out of 100—for every pick. In that case, we can use the Simple Product Rule for our calculation:
P(R1 ∨ R2 ∨ R3 ∨ R4) = 1 – [P(~ R1) x P(~ R2) x P(~ R3) x P(~ R4)]
Since there are 20 red marbles, there are 80 non-red marbles, so the probability of picking a color other than red on any given selection is .8.
P(R1 ∨ R2 ∨ R3 ∨ R4) = 1 – (.8 x .8 x .8 x .8)
= 1 – .4096
= .5904
If we don’t replace the marbles after each selection, then the events are not independent, and we must use the General Product Rule for our calculation. The quantity that we subtract from 1 will be this:
P(~ R1) x P(~ R2 | ~ R1) x P(~ R3 | ~ R1 • ~ R2) x P(~ R4 | ~ R1 • ~ R2 • ~ R3) = ?
On the first selection, our chances of picking a non-red marble are 80/100. On the second selection, assuming we chose a non-red marble the first time, our chances are 79/99. And on the third and fourth selections, the probabilities are 78/98 and 77/97, respectively. Multiplying all these together, we get .4033 (approximately), and so our calculation of the probability of getting at least one red marble looks like this:
P(R1 ∨ R2 ∨ R3 ∨ R4) = 1 – .4033 = .5967 (approximately)
We have a slightly better chance at getting a red marble if we don’t replace them, since each selection of a non-red marble makes the urn’s composition a little more red-heavy.
EXERCISES
- Flip a coin 6 times; what’s the probability of getting heads every time?
- Go into a racquetball court and use duct tape to divide the floor into four quadrants of equal area. Throw three super-balls in random directions against the walls as hard as you can. What’s the probability that all three balls come to rest in the same quadrant?
- You’re at your grandma’s house for Christmas, and there’s a bowl of holiday-themed M&Ms— red and green ones only. There are 500 candies in the bowl, with equal number of each color. Pick one, note its color, then eat it. Pick another, note its color, and eat it. Pick a third, note its color, and eat it. What’s the probability that you ate three straight red M&Ms?
- You and two of your friends enter a raffle. There is one prize: a complete set of Ultra Secret Rare Pokémon cards. There are 1000 total tickets sold; only one is the winner. You buy 20, and your friends each buy 10. What’s the probability that one of you wins those Pokémon cards?
- You’re a 75% free-throw shooter. You get fouled attempting a 3-point shot, which means you get 3 free-throw attempts. What’s the probability that you make at least one of them?
- Roll two dice; what’s the probability of rolling a seven? How about an eight?
- In my county, 70% of people believe in Big Foot. Pick three people at random. What’s the probability that at least one of them is a believer in Big Foot?
- You see these two boxes here on the table? Each of them has jelly beans inside. We’re going to play a little game, at the end of which you have to pick a random jelly bean and eat it. Here’s the deal with the jelly beans. You may not be aware of this, but food scientists are able to create jelly beans with pretty much any flavor you want—and many you don’t want. There is, in fact, such a thing as vomit-flavored jelly beans.[6] Anyway, in one of my two boxes, there are 100 total jelly beans, 8 of which are vomit-flavored (the rest are normal fruit flavors). In the other box, I have 50 jelly beans, 7 of which are vomit-flavored. Remember, this all ends with you choosing a random jelly bean and eating it. But you have a choice between two methods of determining how it will go down: (a) You flip a coin, and the result of the flip determines which of the two boxes you choose a jelly bean from; (b) I dump all the jelly beans into the same box and you pick from that. Which option do you choose? Which one minimizes the probability that you’ll end up eating a vomit-flavored jelly bean? Or does it not make any difference?
- For men entering college, the probability that they will finish a degree within four years is .329; for women, it’s .438. Consider two freshmen—Albert and Betty. What’s the probability that at least one of them will fail to complete college in at least four years? What’s the probability that exactly one of them will succeed in doing so?
- I love Chex Mix. My favorite things in the mix are those little pumpernickel chips. But they’re relatively rare compared to the other ingredients. That’s OK, though, since my second-favorite are the Chex pieces themselves, and they’re pretty abundant. I don’t know what the exact ratios are, but let’s suppose that it’s 50% Chex cereal, 30% pretzels, 10% crunchy bread sticks, and 10% my beloved pumpernickel chips. Suppose I’ve got a big bowl of Chex Mix: 1,000 total pieces of food. If I eat three pieces from the bowl, (a) what’s the probability that at least one of them will be a pumpernickel chip? And (b) what’s the probability that either all three will be pumpernickel chips or all three will be my second-favorite—Chex pieces?
- You’re playing draw poker. Here’s how the game works: a poker hand is a combination of five cards; some combinations are better than others; in draw poker, you’re dealt an initial hand, and then, after a round of wagering, you’re given a chance to discard some of your cards (up to three) and draw new ones, hoping to improve your hand; after another round of betting, you see who wins. In this particular hand, you’re initially dealt a 7 of hearts and the 4, 5, 6, and King of spades. This hand is quite weak on its own, but it’s very close to being quite strong, in two ways: it’s close to being a “flush”, which is five cards of the same suit (you have four spades); it’s also close to being a “straight”, which is five cards of consecutive rank (you have four in a row in the 4, 5, 6, and 7). A flush beats a straight, but in this situation that doesn’t matter; based on how the other players acted during the first round of betting, you’re convinced that either the straight or the flush will win the money in the end. The question is, which one should you go for? Should you discard the King, hoping to draw a 3 or an 8 to complete your straight? Or should you discard the 7 of hearts, hoping to draw a spade to complete your flush? What’s the probability for each? You should pick whichever one is higher.[7]
II. Probability and Decision-Making: Value and Utility
The future is uncertain, but we have to make decisions every day that have an effect on our prospects, financial and otherwise. Faced with uncertainty, we do not merely throw up our hands and guess randomly about what to do; instead, we assess the potential risks and benefits of a variety of options, and choose to act in a way that maximizes the probability of a beneficial outcome. Things won’t always turn out for the best, but we have to try to increase the chances that they will. To do so, we use our knowledge—or at least our best estimates—of the probabilities of future events to guide our decisions.
The process of decision-making in the face of uncertainty is most clearly illustrated with examples involving financial decisions. When we make a financial investment, or—what’s effectively though not legally the same thing—a wager, we’re putting money at risk with the hope that it will pay off in a larger sum of money in the future. We need a way of deciding whether such bets are good ones or not. Of course, we can evaluate our financial decisions in hindsight, and deem the winning bets good choices and the losing ones bad choices, but that’s not a fair standard. The question is, knowing what we knew at the time we made our decision, did we make the choice that maximized the probability of a profitable outcome, even if the profit was not guaranteed?
To evaluate the soundness of a wager or investment, then, we need to look not at its worth after the fact—its final value, we might say—but rather at the value we can reasonably expect it to have in the future, based on what we know at the time the decision is made. We’ll call this the expected value. To calculate the expected value of a wager or investment, we must take into consideration (a) the various possible ways in which the future might turn out that are relevant to our bet, (b) the value of our investment in those various circumstances, and (c) the probabilities that these various circumstances will come to pass. The expected value is a weighted average of the values in the different circumstances; it is weighted by the probabilities of each circumstance. Here is how we calculate expected value (EV):
EV = P(O1) x V(O1) + P(O2) x V(O2) + … + P(On) x V(On)
This formula is a sum; each term in the sum is the product of a probability and a value. The terms ‘O1, O2, …, On’ refer to all the possible future outcomes that are relevant to our bet. P(Ox) is the probability that outcome #x will come to pass. V(Ox) is the value of our investment should outcome #x come to pass.
Perhaps the simplest possible scenario we can use to illustrate how this calculation works is the following: you and your roommate are bored, so you decide to play a game; you’ll each put up a dollar, then flip a coin; if it comes up heads, you win all the money; if it comes up tails, she does.[8] What’s the expected value of your $1 bet? First, we need to consider which possible future circumstances are relevant to your bet’s value. Clearly, there are two: the coin comes up heads, and the coin comes up tails. There are two outcomes in our formula: O1 = heads, O2 = tails. The probability of each of these is 1/2. We must also consider the value of your investment in each of these circumstances. If heads comes up, the value is $2—you keep your dollar and snag hers, too. If tails comes up, the value is $0—you look on in horror as she pockets both bills. (Note: value is different from profit. You make a profit of $1 if heads comes up, and you suffer a loss of $1 if tails does—or your profit is -$1. Value is how much money you’re holding at the end.) Plugging the numbers into the formula, we get the expected value:
EV = P(heads) x V(heads) + P(tails) x V(tails) = 1/2 x $2 + 1/2 x $0 = $1
The expected value of your $1 bet is $1. You invested a dollar with the expectation of a dollar in return. This is neither a good nor a bad bet. A good bet is one for which the expected value is greater than the amount invested; a bad bet is one for which it’s less.
This suggests a standard for evaluating financial decisions in the real world: people should look to put their money to work in such a way that the expected value of their investments is as high as possible (and, of course, higher than the invested amount). Suppose I have $1,000 free to invest. One way to put that money to work would be to stick it in a money market account, which is a special kind of savings deposit account one can open with a bank. Such accounts offer a return on your investment in the form of a payment of a certain amount of interest—a percentage of your deposit amount. Interest is typically specified as a yearly rate. So a money market account offering a 1% rate pays me 1% of my deposit amount after a year.[9] Let’s calculate the expected value of an investment of my $1,000 in such an account. We need to consider the possible outcomes that are relevant to my investment. I can only think of two possibilities: at the end of the year, the bank pays me my money; or, at the end of the year, I get stiffed—no money. The calculation looks like this:
EV = P(paid) x V(paid) + P(stiffed) x V(stiffed)
One of the things that makes this kind of investment attractive is that it’s virtually risk-free. Bank deposits of up to $250,000 are insured by the federal government.[10] So even if the bank goes out of business before I withdraw my money, I’ll still get paid in the end.[11] That means P(paid) = 1 and P(stiffed) = 0. Nice. What’s the value when I get paid? It’s the initial $1,000 plus the 1% interest. 1% of $1,000 is $10, so V(paid) = $1,010.
That’s not much of a return, but interest rates are low these days, and it’s not a risky investment. We could increase the expected value if we put our money into something that’s not a sure thing. One option is corporate bonds. For this type of investment, you lend your money to a company for a specified period of time (and they use it to build a factory or something), then you get paid back the principal investment plus some interest.12 Corporate bonds are a riskier investment than bank deposits because they’re no insured by the federal government. If you company goes bankrupt before the date you’re supposed to get paid back, you lose your money. That is, P(paid) in the expected value calculation above is no longer 1; P(stiffed) is somewhere north of 0. What are the relevant probabilities? Well, it depends on the company. There are firms in the “credit rating” business—Moody’s, S&P, Fitch, etc.—that put out reports and classify companies according to how risky they are to loan money to. They assign ratings like ‘AAA’ (or ‘Aaa’, depending on the agency), ‘AA’, ‘BBB’, ‘CC’, and so on. The further into the alphabet you get, the higher the probability you’ll get stiffed. It’s impossible to say exactly what that probability is, of course; the credit rating agencies provide a rough guide, but ultimately it’s up to the individual investor to decide what the risks are and whether they’re worth it.
To determine whether the risks are worth it, we must compare the expected value of an investment in a corporate bond with a baseline, risk-free investment—like our money market account above. Since the probability of getting paid is less than 1, we must have a higher yield than 1% to justify choosing the corporate bond over the safer investment. How much higher? It depends on the company; it depends on how likely it is that we’ll get paid back in the end.
The expected value calculation is simple in these kinds of cases. Even though P(stiffed) is not 0, V(stiffed) is; if we get stiffed, our investment is worth nothing. So when calculating expected value, we can ignore the second term in the sum. All we have to do is multiply P(paid) by V(paid).
Suppose we’re considering investing in a really reliable company; let’s say P(paid) = .99. Doing the math, in order for a corporate bond with this reliable company to be a better bet than a money market account, they’d have offer an interest rate of a little more than 2%. If we consider a less reliable company—say one for which P(paid) = .95—then we’d need a rate of little more than
when George is about to leave on his honeymoon, but he has to go back to the Bailey Building and Loan to prevent such a catastrophe. Anyway, if everybody knows they’ll get their money back even if the bank goes under, such things won’t happen; that’s what the FDIC is for.
Unless, of course, the federal government goes out of business. But in that case, $1,000 is useful maybe as emergency toilet paper; I need canned goods and ammo at that point.
Again, there are all sorts of complications we’re glossing over to keep things simple.
Probably. There are different kinds of bankruptcies and lots of laws governing them; it’s possible for investors to get some money back in probate court. But it’s complicated. One thing’s for sure: our measly $1,000 imaginary investment makes us too small-time to have much of a chance of getting paid during bankruptcy proceedings. 14 Historical data on the probability of default for companies at different ratings by agency are available.
6.3% to make this a better investment. If we go down to a 90% chance of getting paid back, we need a yield of more than 12% to justify that decision.
What does it mean to be a good, rational economic agent? How should a person, generally speaking, invest money? As we mentioned earlier, a plausible rule governing such decisions would be something like this: always choose the investment for which expected value is maximized.
But real people deviate from this rule in their monetary decisions, and it’s not at all clear that they’re irrational to do so. Consider the following choice: (a) we’ll flip a coin, and if it comes up heads, you win $1,000, but if it comes up tails, you win nothing; (b) no coin flip, you just win $499, guaranteed. The expected value of choice (b) is just the guaranteed $499. The value of choice (a) can be easily calculated:
EV = P(heads) x V(heads) + P(tails) x V(tails)
= (.5 x $1,000) + (.5 x $0)
= $500
So according to our principle, it’s always rational to choose (a) over (b): $500 > $499. But in real life, most people who are offered such a choice go with the sure-thing, (b). (If you don’t share that intuition, try upping the stakes—coin flip for $10,000 vs. $4,999 for sure.) Are people who make such a choice behaving irrationally?
Not necessarily. What such examples show is that people take into consideration not merely the value, in dollars, of various choices, but the subjective significance of their outcomes—the degree to which they contribute to the person’s overall well-being. As opposed to ‘value’, we use the term ‘utility’ to refer to such considerations. In real life decisions, what matters is not the expected value of an investment choice, but its expected utility—the degree to which it satisfies a person’s desires, comports with subjective preferences.
The tendency of people to accept a sure thing over a risky wager, despite a lower expected value, is referred to as risk aversion. This is the consequence of an idea first formalized by the mathematician Daniel Bernoulli in 1738: the diminishing marginal utility of wealth. The basic idea is that as the amount of money one has increases, each addition to one’s fortune becomes less important, from a personal, subjective point of view. An extra $1,000 means very little to Bill Gates; an extra $1,000 for a poor college student would mean quite a lot. The money would add very little utility for Gates, but much more for the college student. Increases in one’s fortune above zero mean more than subsequent increases. Bernoulli’s utility function looked something like this[12]:
Diminishing Marginal Utility of Wealth
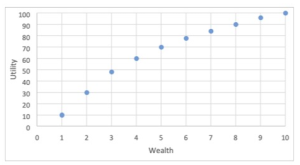
This explains the choice of the $499 sure-thing over the coin flip for $1,000. The utility attached to those first $499 is greater than the extra utility of the additional possible $501 dollars one could potentially win, so people opt to lock in the gain. Utility rises quickly at first, but levels out at higher amounts. From Bernoulli’s chart, the utility of the sure-thing is somewhere around 70, while the utility of the full $1,000 is only 30 more—100. Computing the expected utility of the coin-flip wager gives us this result:
EU = P(heads) x U(heads) + P(tails) x U(tails)
= (.5 x 100) + (.5 x 0)
= 50
The utility of 70 for the sure-thing easily beats the expected utility from the wager. It is possible to get people to accept risky bets over sure-things, but one must take into account this diminishing marginal utility. For a person whose personal utility function is like Bernoulli’s, an offer of a mere $300 (where the utility is down closer to 50) would make the decision more difficult. An offer of $200 would cause them to choose the coin flip.
It has long been accepted economic doctrine that rational economic agents act in such a way as to maximize their utility, not their value. It is a matter of some dispute what sort of utility function best captures rational economic agency. Different economic theories assume different versions of ideal rationality for the agents in their models.
Recently, this practice of assuming perfect utility-maximizing rationality of economic agents has been challenged. While it’s true that the economic models generated under such assumptions can provide useful results, as a matter of fact, the behavior of real people (homo sapiens as opposed to “homo economicus”—the idealized economic man of the models) departs in predictable ways from the utility-maximizing ideal. Psychologists—especially Daniel Kahneman and Amos Tversky— have conducted a number of experiments that demonstrate pretty conclusively that people regularly behave in ways that, by the lights of economic theory, are irrational. For example, consider the following two scenarios (go slowly; think about your choices carefully):
You have $1,000. Which would you choose?
Coin flip. Heads, you win another $1,000; tails, you win nothing.
An additional $500 for sure.
You have $2,000. Which would you choose?
Coin flip. Heads you lose $1,000; tails, you lose nothing.
Lose $500 for sure.[13]
According to the Utility Theory of Bernoulli and contemporary economics, the rational agent would choose option (b) in each scenario. Though they start in different places, for each scenario option (a) is just a coin flip between $1,000 and $2,000, while (b) is $1,500 for sure. Because of the diminishing marginal utility of wealth, (b) is the utility-maximizing choice each time. But as a matter of fact, most people choose option (b) only in the first scenario; they choose option (a) in the second. (If you don’t share this intuition, try upping the stakes.) It turns out that most people dislike losing more than they like winning, so the prospect of a guaranteed loss in 2(b) is repugnant. Another example: would you accept a wager on a coin flip, where heads wins you $1,500, but tails loses you $1,000? Most people would not. (Again, if you’re different, try upping the stakes.) And this despite the fact that clearly expected value and utility point to accepting the proposition.
Kahneman and Tversky’s alternative to Utility Theory is called “Prospect Theory”. It accounts for these and many other observed regularities in human economic behavior. For example, people’s willingness to overpay for a very small chance at a very large gain (lottery tickets); also, their willingness to pay a premium to eliminate small risks (insurance); their willingness to take on risk to avoid large losses; and so on.[14]
It’s debatable whether the observed deviations from idealized utility-maximizing behavior are rational or not. The question “What is an ideally rational economic agent?” is not one that we can answer easily. That’s a question for philosophers to grapple with. The question that economists are grappling with is whether, and to what extent, they must incorporate these psychological regularities into their models. Real people are not the utility-maximizers the models say they are. Can we get more reliable economic predictions by taking their actual behavior into account? Behavioral economics is the branch of that discipline that answers this question in the affirmative. It is a rapidly developing field of research.
EXERCISES
- You buy a $1 ticket in a raffle. There are 1,000 tickets sold. Tickets are selected out of one of those big round drums at random. There are 3 prizes: first prize is $500; second prize is $200; third prize is $100. What’s the expected value of your ticket?
- On the eve of the 2016 U.S. presidential election, the poll-aggregating website 538.com predicted that Donald Trump had a 30% chance of winning. It’s possible to wager on these sorts of things, believe it or not (with bookmakers or in “prediction markets”). On election night, right before 8:00pm EST, the “money line” odds on a Trump victory were +475. That means that a wager of $100 on Trump would earn $475 in profit, for a total final value of $575. Assuming the 538.com crew had the probability of a Trump victory right, what was the expected value of a $100 wager at 8:00pm at the odds listed?
- You’re offered three chances to roll a one with a fair die. You put up $10 and your challenger puts up $10. If you succeed in rolling one even once, you win all the money; if you fail, your challenger gets all the money. Should you accept the challenge? Why or why not?
- You’re considering placing a wager on a horse race. The horse you’re considering is a longshot; the odds are 19 to 1. That means that for every dollar you wager, you’d win $19 in profit (which means $20 total in your pocket afterwards). How probable must it be that the horse will win for this to be a good wager (in the sense that the expected value is greater than the amount bet)?
- I’m looking for a good deal in the junk bond market. These are highly risky corporate bonds; the risk is compensated for with higher yields. Suppose I find a company that I think has a 25% chance of going bankrupt before the bond matures. How high of a yield do I need to be offered to make this a good investment (again, in the sense that the expected value is greater than the price of the investment)?
- For someone with a utility function like that described by Bernoulli (see above), what would their choice be if you offered them the following two options: (a) coin flip, with heads winning $8,000 and tails winning $2,000; (b) $5,000 guaranteed? Explain why they would make that choice, in terms of expected utility. How would increasing the lower prize on the coin-flip option change things, if at all? Suppose we increased it to $3,000. Or $4,000. Explain your answers.
III. Probability and Belief: Bayesian Reasoning
The great Scottish philosopher David Hume, in his An Enquiry Concerning Human Understanding, wrote, “In our reasonings concerning matter of fact, there are all imaginable degrees of assurance, from the highest certainty to the lowest species of moral evidence. A wise man, therefore, proportions his belief to the evidence.” Hume is making a very important point about a kind of reasoning that we engage in every day: the adjustment of beliefs in light of evidence. We believe things with varying degrees of certainty, and as we make observations or learn new things that bear on those beliefs, we make adjustments to our beliefs, becoming more or less certain accordingly. Or, at least, that’s what we ought to do. Hume’s point is an important one because too often people do not adjust their beliefs when confronted with evidence—especially evidence against their cherished opinions. One needn’t look far to see people behaving in this way: the persistence and ubiquity of the beliefs, for example, that vaccines cause autism, or that global warming is a myth, despite overwhelming evidence to the contrary, are a testament to the widespread failure of people to proportion their beliefs to the evidence, to a general lack of “wisdom”, as Hume puts it.
Here we have a reasoning process—adjusting beliefs in light of evidence—which can be done well or badly. We need a way to distinguish good instances of this kind of reasoning from bad ones. We need a logic. As it happens, the tools for constructing such a logic are ready to hand: we can use the probability calculus to evaluate this kind of reasoning.
Our logic will be simple: it will be a formula providing an abstract model of perfectly rational belief-revision. The formula will tell us how to compute a conditional probability. It’s named after the 18th century English reverend who first formulated it: Thomas Bayes. It is called “Bayes’ Law” and reasoning according to its strictures is called “Bayesian reasoning”.
At this point, you will naturally be asking yourself something like this: “What on Earth does a theorem about probability have to do with adjusting beliefs based on evidence?” Excellent question; I’m glad you asked. As Hume mentioned in the quote we started with, our beliefs come with varying degrees of certainty. Here, for example, are three things I believe: (a) 1 + 1 = 2; (b) the earth is approximately 93 million miles from the sun (on average); (c) I am related to Winston Churchill. I’ve listed them in descending order: I’m most confident in (a), least confident in (c). I’m more confident in (a) than (b), since I can figure out that 1 + 1 = 2 on my own, whereas I have to rely on the testimony of others for the Earth-to-Sun distance. Still, that testimony gives me a much stronger belief than does the testimony that is the source of (c). My relation to Churchill is apparently through my maternal grandmother; the details are hazy. Still, she and everybody else in the family always said we were related to him, so I believe it.
“Fine,” you’re thinking, “but what does this have to do with probabilities?” Our degrees of belief in particular claims can vary between two extremes: complete doubt and absolute certainty. We could assign numbers to those states: complete doubt is 0; absolute certainty is 1. Probabilities also vary between 0 and 1! It’s natural to represent degrees of beliefs as probabilities. This is one of the philosophical interpretations of what probabilities really are.[15] It’s the so-called “subjective” interpretation, since degrees of belief are subjective states of mind; we call these “personal probabilities”. Think of rolling a die. The probability that it will come up showing a one is 1/6. One way of understanding what that means is to say that, before the die was thrown, the degree to which you believed the proposition that the die will come up showing one—the amount of confidence you had in that claim—was 1/6. You would’ve had more confidence in the claim that it would come up showing an odd number—a degree of belief of 1/2.
We’re talking about the process of revising our beliefs when we’re confronted with evidence. In terms of probabilities, that means raising or lowering our personal probabilities as warranted by the evidence. Suppose, for example, that I was visiting my grandmother’s hometown and ran into a friend of hers from way back. In the course of the conversation, I mention how grandma was related to Churchill. “That’s funny,” says the friend, “your grandmother always told me she was related to Mussolini.” I’ve just received some evidence that bears on my belief that I’m related to Churchill. I never heard this Mussolini claim before. I’m starting to suspect that my grandmother had an odd eccentricity: she enjoyed telling people that she was related to famous leaders during World War II. (I wonder if she ever claimed to be related to Stalin. FDR? Let’s pray Hitler was never invoked. And Hirohito would strain credulity; my grandma was clearly not Japanese.) In response to this evidence, if I’m being rational, I would revise my belief that I’m related to Winston Churchill: I would lower my personal probability for that belief; I would believe it less strongly. If, on the other hand, my visit to my grandma’s hometown produced a different bit of evidence— let’s say a relative had done the relevant research and produced a family genealogy tracing the relation to Churchill—then I would revise my belief in the other direction, increasing my personal probability, believing it more strongly.
Since belief-revision in this sense just involves adjusting probabilities, our model for how it works is just a means of calculating the relevant probabilities. That’s why our logic can take the form of an equation. We want to know how strongly we should believe something, given some evidence about it. That’s a conditional probability. Let ‘H’ stand for a generic hypothesis—something we believe to some degree or other; let ‘E’ stand for some evidence we discover. What we want to know is how to calculate P(H | E)—the probability of H given E, how strongly we should believe H in light of the discovery of E.
Bayes’ Law tells us how to perform this calculation. Here’s one version of the equation:[16]
P(H) x P(E | H)
P(H | E) = —————————-
P(E)
This equation has some nice features. First of all, the presence of ‘P(H)’ in the numerator is intuitive. This is often referred to as the “prior probability” (or “prior” for short); it’s the degree to which the hypothesis was believed prior to the discovery of the evidence. It makes sense that this would be part of the calculation: how strongly I believe in something now ought to be (at least in part) a function of how strongly I used to believe it. Second, ‘P(E | H)’ is a useful item to have in the calculation, since it’s often a probability that can be known. Notice, this is the reverse of the conditional probability we’re trying to calculate: it’s the probability of the evidence, assuming that the hypothesis is true (it may not be, but we assume it is, as they say, “for the sake of argument”). Consider an example: as you may know, being sick in the morning can be a sign of pregnancy; if this were happening to you, the hypothesis you’d be entertaining would be that you’re pregnant, and the evidence would be vomiting in the morning. The conditional probability you’re interested in is P(pregnant | vomiting)—that is, the probability that you’re pregnant, given that you’ve been throwing up in the morning. Part of using Bayes’ Law to make this calculation involves the reverse of that conditional probability: P(vomiting | pregnant)—the probability that you’d be throwing up in the morning, assuming (for the sake of argument) that you are in fact pregnant. And that’s something we can just look up; studies have been done. It turns out that about 60% of women experience have morning sickness (to the point of throwing up) during the first trimester of pregnancy. There are lots of facts like this available. Did you know that a craving for ice is a potential sign of anemia? Apparently it is: 44% of anemia patients have the desire to eat ice. Similar examples are not hard to find. It’s worth noting, in addition, that sometimes the reverse probability in question—P(E | H)—is 1. In the case of a prediction made by a scientific hypothesis, this is so. Isaac Newton’s theory of universal gravitation, for example, predicts that objects dropped from the same height will take the same amount of time to reach the ground, regardless of their weights (provided that air resistance is not a factor). This prediction is just a mathematical result of the equation governing gravitational attraction. So if H is Newton’s theory and E is a bowling ball and a feather taking the same amount of time to fall, then P(E | H) = 1; if Newton’s theory is true, then it’s a mathematical certainty that the evidence will be observed.[17]
So this version of Bayes’ Law is attractive because of both probabilities in the numerator: P(H), the prior probability, is natural, since the adjusted degree of belief ought to depend on the prior degree of belief; and P(E | H) is useful, since it’s a probability that we can often know precisely. The formula is also nice in that it comports well with our intuitions about how belief-revision ought to work. It does this in three ways.
First, we know that implausible hypotheses are hard to get people to believe; as Carl Sagan once put it, “Extraordinary claims require extraordinary evidence.” Putting this in terms of personal probabilities, an implausible hypothesis—and extraordinary claim—is just one with a low prior: P(H) is a small fraction. Consider an example. In the immediate aftermath of the 2358 U.S. presidential election, some people claim that the election was rigged (possibly by Mars) in favor of General Krang by way of a massive computer hacking scheme that manipulated the vote totals in key precincts.22 You have very little confidence in this hypothesis— and give it an extremely low prior probability—for lots of reasons, but two in particular: (a) Voting machines in individual precincts are not networked together, so any hacking scheme would have to be carried out on a machine-by-machine basis across hundreds—if not thousands—of precincts, an operation of almost impossible complexity; (b) An organization with practically unlimited financial resources and the strongest possible motivation for uncovering such a scheme—namely, the anti-Krang campaign—looked at the data and concluded there was nothing fishy going on. But none of this stops wishful-thinking anti-Krang voters from digging for evidence that in fact the fix had been in for Krang. When people approach you with this kind of evidence—look at these suspiciously high turnout numbers from a handful of precincts in rural Wisconsin!— your degree of belief in the hypothesis—that the Martians had hacked the election—barely budges. This is proper; again, extraordinary claims require extraordinary evidence, and future you isn’t seeing it. This intuitive fact about how belief-revision is supposed to work is borne out by the equation for Bayes’ Law. Implausible hypotheses have a low prior—P(H) is a small fraction. It’s hard to increase our degree of belief in such propositions—P(H | E) doesn’t easily rise—simply because we’re multiplying by a low fraction in the numerator when calculating the new probability.
The math mirrors the actual mechanics of belief-revision in two more ways. Here’s a truism: the more strongly predictive piece of evidence is for a given hypothesis, the more it supports that hypothesis when we observe it. We saw above that women who are pregnant experience morning sickness about 60% of the time; also, patients suffering from anemia crave ice (for some reason) 44% of the time. In other words, throwing up in the morning is more strongly predictive of pregnancy than ice-craving is of anemia. Morning sickness would increase belief in the hypothesis of pregnancy more than ice-craving would increase belief in anemia. Again, this banal observation is borne out in the equation for Bayes’ Law. When we’re calculating how strongly we should believe in a hypothesis in light of evidence—P(H | E)—we always multiply in the numerator by the reverse conditional probability—P(E | H)—the probability that you’d observe the evidence, assuming the hypothesis is true. For pregnancy/sickness, this means multiplying by .6; for anemia/ice-craving, we multiply by .44. In the former case, we’re multiplying by a higher number, so our degree of belief increases more.
A third intuitive fact about belief-revision that our equation correctly captures is this: surprising evidence provides strong confirmation of a hypothesis. Consider the example of Albert Einstein’s general theory of relativity, which provided a new way of understanding gravity: the presence of massive objects in a particular region of space affects the geometry of space itself, causing it to be curved in that vicinity. Einstein’s theory has a number of surprising consequences, one of which is that because space is warped around massive objects, light will not travel in a straight line in those places.[18] In this example, H is Einstein’s general theory of relativity, and E is an observation of light following a curvy path. When Einstein first put forward his theory in 1915, it was met with incredulity by the scientific community, not least because of this astonishing prediction. Light bending? Crazy! And yet, four years later, Arthur Eddington, an English astronomer, devised and executed an experiment in which just such an effect was observed. He took pictures of stars in the night sky, then kept his camera trained on the same spot and took another picture during an eclipse of the sun (the only time the stars would also be visible during the day). The new picture showed the stars in slightly different positions, because during the eclipse, their light had to pass near the sun, whose mass caused their path to be deflected slightly, just as Einstein predicted. As soon as Eddington made his results public, newspapers around the world announced the confirmation of general relativity and Einstein became a star. As we said, surprising results provide strong confirmation; hardly anything could be more surprising that light bending. We can put this in terms of personal probabilities. Bending light was the evidence, so P(E) represents the degree of belief someone would have in the proposition that light will travel a curvy path. This was a very low number before Eddington’s experiments. When we use is to calculate how strongly we should believe in general relativity given the evidence that light in fact bends—P(H | E)—it’s in the denominator of our equation. Dividing by a very small fraction means multiplying by its reciprocal, which is a very large number. This makes P(H | E) go up dramatically. Again, the math mirrors actual reasoning practice.
So, our initial formulation of Bayes’ Law has a number of attractive features; it comports well with our intuitions about how belief-revision actually works. But it is not the version of Bayes’ Law that we will settle on the make actual calculations. Instead, we will use a version that replaces the denominator—P(E)—with something else. This is because that term is a bit tricky. It’s the prior probability of the evidence. That’s another subjective state—how strongly you believed the evidence would be observed prior to its actual observation, or something like that. Subjectivity isn’t a bad thing in this context; we’re trying to figure out how to adjust subjective states (degrees of belief), after all. But the more of it we can remove from the calculation, the more reliable our results. As we discussed, the subjective prior probability for the hypothesis in question—P(H)— belongs in our equation: how strongly we believe in something now ought to be a function of how strongly we used to believe in it. The other item in the numerator—P(E | H)—is most welcome, since it’s something we can often just look up—an objective fact. But P(E) is problematic. It makes sense in the case of light bending and general relativity. But consider the example where I run into my grandma’s old acquaintance and she tells me about her claims to be related to Mussolini. What was my prior for that? It’s not clear there even was one; the possibility probably never even occurred to me. I’d like to get rid of the present denominator and replace it with the kinds of terms I like—those in the numerator.
I can do this rather easily. To see how, it will be helpful to consider the fact that when we’re evaluating a hypothesis in light of some evidence, there are often alternative hypotheses that it’s competing with. Suppose I’ve got a funny looking rash on my skin; this is the evidence. I want to know what’s causing it. I may come up with a number of possible explanations. It’s winter, so maybe it’s just dry skin; that’s one hypothesis. Call it ‘H1’. Another possibility: we’ve just started using a new laundry detergent at my house; maybe I’m having a reaction. H2 = detergent. Maybe it’s more serious, though. I get on the Google and start searching. H3 = psoriasis (a kind of skin disease). Then my hypochondria gets out of control, and I get really scared: H4 = leprosy. That’s all I can think of, but it may not be any of those: H5 = some other cause.
I’ve got five possible explanations for my rash—five hypotheses I might believe in to some degree in light of the evidence. Notice that the list is exhaustive: since I added H5 (something else), one of the five hypotheses will explain the rash. Since this is the case, we can say with certainty that I have a rash and it’s caused by the cold, or I have a rash and it’s caused by the detergent, or I have a rash and it’s caused by psoriasis, or I have a rash and it’s caused by leprosy, or I have a rash and it’s caused by something else. Generally speaking, when a list of hypotheses is exhaustive of the possibilities, the following is a truth of logic:
E ≡ (E • H1) ∨ (E • H2) ∨ … ∨ (E • Hn)
For each of the conjunctions, it doesn’t matter what order you put the conjuncts, so this true, too:
E ≡ (H1 • E) ∨ (H2 • E) ∨ … ∨ (Hn • E)
Remember, we’re trying to replace P(E) in the denominator of our formula. Well, if E is equivalent to that long disjunction, then P(E) is equal to the probability of the disjunction:
P(E) = P[(H1 • E) (H2 • E) … (Hn • E)]
We’re calculating a disjunctive probability. If we assume that the hypotheses are mutually exclusive (only one of them can be true), then we can use the Simple Addition Rule:[19]
P(E) = P(H1 • E) + P(H2 • E) + … + P(Hn • E)
Each item in the sum is a conjunctive probability calculation, for which we can use the General Product Rule:
P(E) = P(H1) x P(E | H1) + P(H2) x P(E | H2) + … + P(Hn) x P(E | Hn)
And look what we have there: each item in the sum is now a product of exactly the two types of terms that I like—a prior probability for a hypothesis, and the reverse conditional probability of the evidence assuming the hypothesis is true (the thing I can often just look up). I didn’t like my old denominator, but it’s equivalent to something I love. So I’ll replace it. This is our final version of Bayes’ Law:
| P(Hk) x P(E | Hk) | ||
| P(Hk | E) = | —————————————————– | [1 ≤ k ≤ n][20] |
| P(H1) x P(E | H1) + P(H2) x P(E | H2) + … + P(Hn) x P(E | Hn) |
Let’s see how this works in practice. Consider the following scenario:
Your mom does the grocery shopping at your house. She goes to two stores: Fairsley Foods and Gibbons’ Market. Gibbons’ in closer to home, so she goes there more often—80% of the time. Fairsley sometimes has great deals, though, so she drives the extra distance and shops there 20% of the time.
You can’t stand Fairsley. First of all, they’ve got these annoying commercials with the crazy owner shouting into the camera and acting like a fool. Second, you got lost in there once when you were a little kid and you’ve still got emotional scars. Finally, their produce section is terrible: in particular, their peaches—your favorite fruit—are often mealy and bland, practically inedible. In fact, you’re so obsessed with good peaches that you made a study of it, collecting samples over a period of time from both stores, tasting and recording your data. It turns out that peaches from Fairsley are bad 40% of the time, while those from Gibbons’ are only bad 20% of the time. (Peaches are a fickle fruit; you’ve got to expect some bad ones no matter how much care you take.)
Anyway, one fine day you walk into the kitchen and notice a heaping mound of peaches in the fruit basket; mom apparently just went shopping. Licking your lips, you grab a peach and take a bite. Ugh! Mealy, bland—horrible. “Stupid Fairsley,” you mutter as you spit out the fruit. Question: is your belief that the peach came from Fairsley rational? How strongly should you believe that it came from that store?
This is the kind of question Bayes’ Law can help us answer. It’s asking us about how strongly we should believe in something; that’s just calculating a (conditional) probability. We want to know how strongly we should believe that the peach came from Fairsley; that’s our hypothesis. Let’s call it ‘F’. These types of calculations are always of conditional probabilities: we want the probability of the hypothesis given the evidence. In this case, the evidence is that the peach was bad; let’s call that ‘B’. So the probability we want to calculate is P(F | B)—the probability that the peach came from Fairsley given that it’s bad.
At this point, we reference Bayes’ Law and plug things into the formula. In the numerator, we want the prior probability for our hypothesis, and the reverse conditional probability of the evidence assuming the hypothesis is true:
P(F) x P(B | F)
P(F | B) = —————————————-
In the denominator, we need a sum, with each term in the sum having exactly the same form as our numerator: a prior probability for a hypothesis multiplied by the reverse conditional probability. The sum has to have one such term for each of our possible hypotheses. In our scenario, there are only two: that the fruit came from Fairsley, or that it came from Gibbons’. Let’s call the second hypothesis ‘G’. Our calculation looks like this:
P(F) x P(B | F)
P(F | B) = ——————————————-
P(F) x P(F | B) + P(G) x P(F | G)
Now we just have to find concrete numbers for these various probabilities in our little story. First, P(F) is the prior probability for the peach coming from Fairsley—that is, the probability that you would’ve assigned to it coming from Fairsley prior to discovering the evidence that it was bad— before you took a bite. Well, we know mom’s shopping habits: 80% of the time she goes to Gibbons’; 20% of the time she goes to Fairsley. So a random piece of food—our peach, for example—has a 20% probability of coming from Fairsley. P(F) = .2. And for that matter, the peach has an 80% probability of coming from Gibbons’, so the prior probability for that hypothesis— P(G)—is .8. What about P(B | F)? That’s the conditional probability that a peach will be bad assuming it came from Fairsley. We know that! You did a systematic study and concluded that 40% of Fairsley’s peaches are bad; P(B | F) = .4. Moreover, your study showed that 20% of peaches from Gibbons’ were bad, so P(G | F) = .2. We can now plug in the numbers and do the calculation:
P(F | B) = (.2 x .4) / ((.2 x .4) + (.8 x .2)) = .08/(.08 + .16) = 1/3
As a matter of fact, the probability that the bad peach you tasted came from Fairsley—the conclusion to which you jumped as soon as you took a bite—is only 1/3. It’s twice as likely that the peach came from Gibbons’. Your belief is not rational. Despite the fact that Fairsley peaches are bad at twice the rate of Gibbons’, it’s far more likely that your peach came from Gibbons’, mainly because your mom does so much more of her shopping there.
So here we have an instance of Bayes’ Law performing the function of a logic—providing a method for distinguishing good from bad reasoning. Our little story, it turns out, depicted an instance of the latter, and Bayes’ Law showed that the reasoning was bad by providing a standard against which to measure it. Bayes’ Law, on this interpretation, is a model of perfectly rational belief-revision. Of course many real-life examples of that kind of reasoning can’t be subjected to the kind of rigorous analysis that the (made up) numbers in our scenario allowed. When we’re actually adjusting our beliefs in light of evidence, we often lack precise numbers; we don’t walk around with a calculator and an index card with Bayes’ Law on it, crunching the numbers every time we learn new things. Nevertheless, our actual practices ought to be informed by Bayesian principles; they ought to approximate the kind of rigorous process exemplified by the formula. We should keep in mind the need to be open to adjusting our prior convictions, the fact that alternative possibilities exist and ought to be taken into consideration, the significance of probability and uncertainty to our deliberations about what to believe and how strongly to believe it. Again, Hume: the wise person proportions belief according to the evidence.
EXERCISES
- Women are twice as likely to suffer from anxiety disorders as men: 8% to 4%. They’re also more likely to attend college: these days, it’s about a 60/40 ratio of women to men. (Are these two phenomena related? That’s a question for another time.) If a random person is selected from my logic class, and that person suffers from an anxiety disorder, what’s the probability that it’s a woman?
- Among Wisconsin residents, 80% are Green Bay Packers fans, 10% are Chicago Bears fans, and 10% favor some other football team (we’re assuming every Wisconsinite has a favorite team). Packer fans aren’t afraid to show their spirit: 75% of them wear clothes featuring the team logo. Bears fans a quite reluctant to reveal their loyalties in such hostile territory, so only 25% of them are obnoxious enough to wear Bears clothes. Fans of other teams aren’t quite as scared: 50% of them wear their teams’ gear. I’ve got a neighbor who does not wear clothes with his favorite team’s logo. Suspicious (FIB?). What’s the probability he’s a Bears fan?
- In my logic class, 20% of students are deadbeats: on exams, they just guess randomly. 60% of the students are pretty good, but unspectacular: they get correct answers 80% of the time. The remaining 20% of the students are geniuses: they get correct answers 100% of the time. I give a true/false exam. Afterwards, I pick one of the completed exams at random; the student got the first two questions correct. What’s the probability that it’s one of the deadbeats?
IV. Basic Statistical Concepts and Techniques
In this section and the next, the goal is equip ourselves to understand, analyze, and criticize arguments using statistics. Such arguments are extremely common; they’re also frequently manipulative and/or fallacious. As Mark Twain once said, “There are three kinds of lies: lies, damned lies, and statistics.” It is possible, however, with a minimal understanding of some basic statistical concepts and techniques, along with an awareness of the various ways these are commonly misused (intentionally or not), to see the “lies” for what they are: bad arguments that shouldn’t persuade us. In this section, we will provide a foundation of basic statistical knowledge. In the next, we will look at various statistical fallacies.
Averages: Mean vs. Median
The word ‘average’ is slippery: it can be used to refer both to the arithmetic mean or the median of a set of values. The mean and median are often different, and when this is the case, use of the word ‘average’ is equivocal. A clever person can use this fact to her rhetorical advantage. We hear the word ‘average’ thrown around quite a bit in arguments: the average family has such-and-such an income, the average student carries such-and-such in student loan debt, and so on. Audiences are supposed to take this fictional average entity to be representative of all the others, and depending on the conclusion she’s trying to convince people of, the person making the argument will choose between mean and median, picking the number that best serves her rhetorical purpose. It’s important, therefore, for the critical listener to ask, every time the word ‘average’ is used, “Does this refer to the mean or the median? What’s the difference between the two? How would using the other affect the argument?”
A simple example can make this clear.[21] I run a masonry contracting business on the side—Logical Constructions (a wholly owned subsidiary of LogiCorp). Including myself, 22 people work at Logical Constructions. This is how much they’re paid per year: $350,000 for me (I’m the boss); $75,000 each for two foremen; $70,000 for my accountant; $50,000 each for five stone masons; $30,000 for the office secretary; $25,000 each for two apprentices; and $20,000 each for ten laborers. To calculate the mean salary at Logical Constructions, we add up all the individual salaries (my $350,000, $75,000 twice since there are two foremen, and so on) and divide by the number of employees. The result is $50,000. To calculate the median salary, we put all the individual salaries in numerical order (ten entries of $20,000 for the laborers, then two entries of $25,000 for the apprentices, and so on) and find the middle number—or, as is the case with our set, which has an even number of entries, the mean of the middle two numbers. The middle two numbers are both $25,000, so the median salary is $25,000.
Now, you may have noticed, a lot of my workers don’t get paid particularly well. In particular, those at the bottom—my ten laborers—are really getting the shaft: $20,000 a year for that kind of back-breaking work is a raw deal. Suppose one day, as I’m driving past our construction site (in the back of my limo, naturally), I notice some outside agitators commiserating with my laborers during their (10-minute) lunch break—you know the type, union organizers, pinko commies (in this story, I’m a greedy capitalist; play along). They’re trying to convince my employees to bargain collectively for higher wages. Now we have a debate: should the workers at Logical Constructions be paid more? I take one side of the issue; the workers and organizers take the other. In the course of making our arguments, we might both refer to the average worker at Logical Constructions. I’ll want to do so in a way that makes it appear that this mythical worker is doing pretty well, and so we don’t need to change anything; the organizers will want to do so in such a way that makes it appear that the average worker isn’t do very well at all. We have two senses of ‘average’ to choose from: mean and median. In this case, the mean is higher, so I will use it: “The average worker at Logical Constructions makes $50,000 per year. That’s a pretty good wage!” My opponents, the union organizers, will counter, using the median: “The average worker at Logical Constructions makes a mere $25,000 per year. Try raising a family on such a pittance!”
A lot hangs on which sense of ‘average’ we pick. This is true in lots of real-life circumstances. For example, household income in the United States is distributed much as salaries are at my fictional Logical Constructions company: those at the top of the range fare much better than those at the bottom.[22] In such circumstances, the mean is higher than the median. In 2014, the mean household income in the U.S. was $72, 641. That’s pretty good! The median, however, was a mere $53, 657. That’s a big difference! “The average family makes about $72,000 per year” sounds a lot better than “The average family makes about $53,000 per year.”
Normal Distributions: Standard Deviation, Confidence Intervals
If you gave IQ tests to a whole bunch of people, and then graphed the results on a histogram or bar chart—so that every time you saw a particular score, the bar for that score would get higher— you’d end up with a picture like this:
This kind of distribution is called a “normal” or “Gaussian” distribution[23]; because of its shape, it’s often called a “bell curve”. Besides IQ, many phenomena in nature are (approximately) distributed normally: height, blood pressure, motions of individual molecules in a collection, lifespans of industrial products, measurement errors, and so on.[24] And even when traits are not normally distributed, it can be useful to treat them as if they were. This is because the bell curve provides an extremely convenient starting point for making certain inferences. It’s convenient because one can know everything about such a curve by specifying two of its features: its mean (which, because the curve is symmetrical, is the same as its median) and its standard deviation.
We already understand the mean. Let’s get a grip on standard deviation. We don’t need to learn how to calculate it (though that can be done); we just want a qualitative (as opposed to quantitative) understanding of what it signifies. Roughly, it’s a measure of the spread of the data represented on the curve; it’s a way of indicating how far, on average, values tend to stray from the mean. An example can make this clear. Consider two cities: Milwaukee, WI and San Diego, CA. These two cities are different in a variety of ways, not least in the kind of weather their residents experience. Setting aside precipitation, let’s focus just on temperature. If you recorded the high temperatures every day in each town over a long period of time and made a histogram for each (with temperatures on the x-axis, number of days on the y-axis), you’d get two very different-looking curves. Maybe something like these:
|
|
|
| Milwaukee | San Diego |
The average high temperatures for the two cities—the peaks of the curves—would of course be different: San Diego is warmer on average than Milwaukee. But the range of temperatures experienced in Milwaukee is much greater than that in San Diego: some days in Milwaukee, the high temperature is below zero, while on some days in the summer it’s over 100°F. San Diego, on the other hand, is basically always perfect: right around 70° or so.[25] The standard deviation of temperatures in Milwaukee is much greater than in San Diego. This is reflected in the shapes of the respective bell curves: Milwaukee’s is shorter and wider—with a non-trivial number of days at the temperature extremes and a wide spread for all the other days—and San Diego’s is taller and narrower—with temperatures hovering in a tight range all year, and hence more days at each temperature recorded (which explains the relative heights of the curves).
Once we know the mean and standard deviation of a normal distribution, we know everything we need to know about it. There are three very useful facts about these curves that can be stated in terms of the mean and standard deviation (SD). As a matter of mathematical fact, 68.3% of the population depicted on the curve (whether they’re people with certain IQs, days on which certain temperatures were reached, measurements with a certain amount of error) falls within a range of one standard deviation on either side of the mean. So, for example, the mean IQ is 100; the standard deviation is 15. It follows that 68.3% of people have an IQ between 85 and 115—15 points (one SD) on either side of 100 (the mean). Another fact: 95.4% of the population depicted on a bell curve will fall within a range two standard deviations from the mean. So 95.4% of people have an IQ between 70 and 130—30 points (2 SDs) on either side of 100. Finally, 99.7% of the population falls within three standard deviations of the mean; 99.7% of people have IQs between 55 and 145. These ranges are called confidence intervals.[26] They are convenient reference points commonly used in statistical inference.[27]
Statistical Inference: Hypothesis Testing
If we start with knowledge of the properties of a given normal distribution, we can test claims about the world to which that information is relevant. Starting with a bell curve—information of a general nature—we can make draw conclusions about particular hypotheses. These are conclusions of inductive arguments; they are not certain, but more or less probable. When we use knowledge of normal distributions to draw them, we can be precise about how probable they are. This is inductive logic.
The basic pattern of the kinds of inferences we’re talking about is this: one formulates a hypothesis, then runs an experiment to test it; the test involves comparing the results of that experiment to what is known (some normal distribution); depending on how well the results of the experiment comport with what would be expected given the background knowledge represented by the bell curve, we draw a conclusion about whether or not the hypothesis is true.
Though they are applicable in a very wide range of contexts, it’s perhaps easiest to explain the patterns of reasoning we’re going to examine using examples from medicine. These kinds of cases are vivid; they aid in understanding by making the consequences of potential errors more real. Also, in these cases the hypotheses being tested are relatively simple: claims about individuals’ health—whether they’re healthy or sick, whether they have some condition or don’t—as opposed to hypotheses dealing with larger populations and measurements of their properties. Examining these simpler cases will allow us to see more clearly the underlying patterns of reasoning that cover all such instances of hypothesis testing, and to gain familiarity with the vocabulary statisticians use in their work.
The knowledge we start with is how some trait relevant to the particular condition is distributed in the population generally—a bell curve.[28] The experiment we run is to measure the relevant trait in the individual whose health we’re assessing. The result of a comparison with the result of this measurement and the known distribution of the trait tells us something about whether or not the person is healthy. Suppose we start with information about how a trait is distributed among people who are healthy. Hematocrit, for example, is a measure of how much of a person’s blood is taken up by red blood cells—expressed as a percentage (of total blood volume). Lower hematocrit levels are associated with anemia; higher levels are associated with dehydration, certain kinds of tumors, and other disorders. Among healthy men, the mean hematocrit level is 47%, with a standard deviation of 3.5%. We can draw the curve, noting the boundaries of the confidence intervals:
spreadsheets to do our math for us makes these confidence intervals more practical. But we’ll stick with the 68.3/95.4/99.7 intervals for simplicity’s sake.34 Again, the actual distribution may not be normal, but we will assume that it is in our examples. The basic patterns of reasoning are similar when dealing with different kinds of distributions.
Hematocrit Levels, Healthy Men
|
|
||||||
| 36.5 | 40 | 43.5 | 47 | 50.5 | 54 | 57.5 |
Because of the fixed mathematical properties of the bell curve, we know that 68.3% of healthy men have hematocrit levels between 43.5% and 50.5%; 95.4% of them are between 40% and 54%; and 99.7% of them are between 36.5% and 57.5%. Let’s consider a man whose health we’re interested in evaluating. Call him Larry. We take a sample of Larry’s blood and measure the hematocrit level. We compare it to the values on the curve to see if there might be some reason to be concerned about Larry’s health. Remember, the curve tells us the levels of hematocrit for healthy men; we want to know if Larry’s one of them. The hypothesis we’re testing is that Larry’s healthy. Statisticians often refer the hypothesis under examination in such tests as the “null hypothesis”—a default assumption, something we’re inclined to believe unless we discover evidence against it. Anyway, we’re measuring Larry’s hematocrit; what kind of result should he be hoping for? Clearly, he’d like to be as close to the middle, fat part of the curve as possible; that’s where most of the healthy people are. The further away from the average healthy person’s level of hematocrit he strays, the more he’s worried about his health. That’s how these tests work: if the result of the experiment (measuring Larry’s hematocrit) is sufficiently close to the mean, we have no reason to reject the null hypothesis (that Larry’s healthy); if the result is far away, we do have reason to reject it.
How far away from the mean is too far away? It depends. A typical cutoff is two standard deviations from the mean—the 95.4% confidence interval.[29] That is, if Larry’s hematocrit level is below 40% or above 54%, then we might say we have reason to doubt the null hypothesis that Larry is healthy. The language statisticians use for such a result—say, for example, if Larry’s hematocrit came in at 38%—is to say that it’s “statistically significant”. In addition, they specify the level at which it’s significant—an indication of the confidence-interval cutoff that was used. In this case, we’d say Larry’s result of 38% is statistically significant at the .05 level. (95% = .95; 1 – .95 = .05) Either Larry is unhealthy (anemia, most likely), or he’s among the (approximately) 5% of healthy people who fall outside of the two standard-deviation range. If he came in at a level even further from the mean—say, 36%—we would say that this result is significant at the .003 level (99.7% = .997; 1 – .997 = .003). That would give us all the more reason to doubt that Larry is healthy.
So, when we’re designing a medical test like this, the crucial decision to make is where to set the cutoff. Again, typically that’s the 95% confidence interval. If a result falls outside that range, the person tests “positive” for whatever condition we’re on the lookout for. (Of course, a “positive” result is hardly positive news—in the sense of being something you want to hear.) But these sorts of results are not conclusive: it may be that the null hypothesis (this person is healthy) is true, and that they’re simply one of the relative rare 5% who fall on the outskirts of the curve. In such a case, we would say that the test has given the person a “false positive” result: the test indicates sickness when in fact there is none. Statisticians refer to this kind of mistake as “type I error”. We could reduce the number of mistaken results our test gives by changing the confidence levels at which we give a positive result. Returning to the concrete example above: suppose Larry has a hematocrit level of 38%, but that he is not in fact anemic; since 38% is outside of the two standard-deviation range, our test would give Larry a false positive result if we used the 95% confidence level. However, if we raised the threshold of statistical significance to the three standard-deviation level of 99.7%, Larry would not get flagged for anemia; there would be no false positive, no type I error.
So we should always use the wider range on these kinds of tests to avoid false positives, right? Not so fast. There’s another kind of mistake we can make: false negatives, or type II errors. Increasing our range increases our risk of this second kind of foul-up. Down there at the skinny end of the curve there are relatively few healthy people. Sick people are the ones who generally have measurements in that range; they’re the ones we’re trying to catch. When we issue a false negative, we’re missing them. A false negative occurs when the test tells you there’s no reason to doubt the null hypothesis (that you’re healthy), when as a matter of fact you are sick. If we increase our range from two to three standard deviations—from the 95% level to the 99.7% level—we will avoid giving a false positive result to Larry, who is healthy despite his low 38% hematocrit level. But we will end up giving false reassurance to some anemic people who have levels similar to Larry’s; someone who has a level of 38% and is sick will get a false negative result if we only flag those outside the 99.7% confidence interval (36.5% – 57.5%).
This is a perennial dilemma in medical screening: how best to strike a balance between the two types of errors—between needlessly alarming healthy people with false positive results and failing to detect sickness in people with false negative results. The terms clinicians use to characterize how well diagnostic tests perform along these two dimensions are sensitivity and specificity. A highly sensitive test will catch a large number of cases of sickness—it has a high rate of true positive results; of course, this comes at the cost of increasing the number of false positive results as well. A test with a high level of specificity will have a high rate of true negative results— correctly identifying healthy people as such; the cost of increased specificity, though, is an increase in the number of false negative results—sick people that the test misses. Since every false positive is a missed opportunity for a true negative, increasing sensitivity comes at the cost of decreasing specificity. And since every false negative is a missed true positive, increasing specificity comes at the cost of decreasing specificity. A final bit of medical jargon: a screening test is accurate to the degree that it is both sensitive and specific.
Given sufficiently thorough information about the distributions of traits among healthy and sick populations, clinicians can rig their diagnostic tests to be as sensitive or specific as they like. But since those two properties pull in opposite directions, there are limits to degree of accuracy that is possible. And depending on the particular case, it may be desirable to sacrifice specificity for more sensitivity, or vice versa.
To see how a screening test might be rigged to maximize sensitivity, let’s consider an abstract hypothetical example. Suppose we knew the distribution of a certain trait among the population of people suffering from a certain disease. (Contrast this with our starting point above: knowledge of the distribution among healthy individuals.) This kind of knowledge is common in medical contexts: various so-called biomarkers—gene mutations, proteins in the blood, etc.—are known to be indicative of certain conditions; often, one can know how such markers are distributed among people with the condition. Again, keeping it abstract and hypothetical, suppose we know that among people who suffer from Disease X, the mean level of a certain biomarker β for the disease is 20, with a standard deviation of 3. We can sum up this knowledge with a curve:
β Levels, People with Disease X
|
|
||||||
| 11 | 14 | 17 | 20 | 23 | 26 | 29 |
Now, suppose Disease X is very serious indeed. It would be a benefit to public health if we were able to devise a screening test that could catch as many cases as possible—a test with a high sensitivity. Given the knowledge we have about the distribution of β among patients with the disease, we can make our test as sensitive as we like. We know, as a matter of mathematical fact, that 68.3% percent of people with the disease have β-levels between 17 and 23; 95.4% of people with the disease have levels between 14 and 26; 99.7% have levels between 11 and 29. Given these facts, we can devise a test that will catch 99.7% of cases of Disease X like so: measure the level of biomarker β in people, and if they have a value between 11 and 29, they get a positive test result; a positive result is indicative of disease. This will catch 99.7% of cases of the condition, because the range chosen is three standard deviations on either side of the mean, and that range contains
99.7% of unhealthy people; if we flag everybody in that range, we will catch 99.7% of cases. Of course, we’ll probably end up catching a whole lot of healthy people as well if we cast our net this wide; we’ll get a lot of false positives. We could correct for this by making our test less sensitive, say by lowering the threshold for a positive test to the two standard-deviation range of 14 – 26. We would now only catch 95.4% of cases of sickness, but we would reduce the number of healthy people given false positives; instead, they would get true negative results, increasing the specificity of our test.
Notice that the way we used the bell curve in our hypothetical test for Disease X was different from the way we used the bell curve in our test of hematocrit levels above. In that case, we flagged people as potentially sick when they fell outside of a range around the mean; in the new case, we flagged people as potentially sick when they fell inside a certain range. This difference corresponds to the differences in the two populations the respective distributions represent: in the case of hematocrit, we started with a curve depicting the distribution of a trait among healthy people; in the second case, we started with a curve telling us about sick people. In the former case, sick people will tend to be far from the mean; in the latter, they’ll tend to cluster closer.
The tension we’ve noted between sensitivity and specificity—between increasing the number of cases our diagnostic test catches and reducing the number of false positives it produces, can be seen when show curves for healthy populations and sick populations in the same graph. There is a biomarker called alpha-fetoprotein in the blood serum of pregnant women. Low levels of this protein are associated with Down syndrome in the fetus; high levels are associated with neural tube defects like open spina bifida (spine isn’t completely inside the body) and anencephaly (hardly any of the brain/skull develops). These are serious conditions—especially those associated with the high levels: if the baby has open spina bifida, you need to be ready for that (with specialists and special equipment) at the time of birth; in cases of anencephaly, the fetus will not be viable (at worst) or will live without sensation or awareness (at best?). Early in pregnancy, these conditions are screened for. Since they’re so serious, you’d like to catch as many cases as possible. And yet, you’d like to avoid alarming false positive results for these conditions. The following chart, with bell curves for healthy babies, those with open spina bifida, and anencephaly, illustrates the difficult tradeoffs in making these sorts of decisions[30]:
The vertical line at 2.5 MoM (multiples of the median) is the typical cutoff for a “positive” result (flagged for potential problems). On the one hand, there are substantial portions of the two curves representing the unhealthy populations—to the left of that line—that won’t be flagged by the test. Those are cases of sickness that we won’t catch—false negatives. On the other hand, there are a whole lot of healthy babies whose parents are going to be unnecessarily alarmed. The area of the “Unaffected” curve to the right of the line may not look like much, but these curves aren’t drawn on a linear scale. If they were, that curve would be much (much!) higher than the two for open spina bifida and anencephaly: those conditions are really rare; there are far more healthy babies. The upshot is, that tiny-looking portion of the healthy curve represents a lot of false positives.
Again, this kind of tradeoff between sensitivity and specificity often presents clinicians with difficult choices in designing diagnostic tests. They must weigh the benefits of catching as many cases as possible against the potential costs of too many false positives. Among the costs are the psychological impacts of getting a false positive. As a parent who experienced it, I can tell you getting news of potential open spina bifida or anencephaly is quite traumatic.[31] But it could be worse. For example, when a biomarker for AIDS was first identified in the mid-1980s, people at the Centers for Disease Control considered screening for the disease among the entire population. The test was sensitive, so they knew they would catch a lot of cases. But they also knew that there would be a good number of false positives. Considering the hysteria that would likely arise from so many diagnoses of the dreaded illness (in those days, people knew hardly anything about AIDS; people were dying of a mysterious illness, and fear and misinformation were widespread), they decided against universal screening. Sometimes the negative consequences of false positives include financial and medical costs. In 2015, the American Cancer Society changed its recommendations for breast-cancer screening: instead of starting yearly mammograms at age 40, women should wait until age 45.[32] This was a controversial decision. Afterwards, many women came forward to testify that their lives were saved by early detection of breast cancer, and that under the new guidelines they may not have fared so well. But against the benefit of catching those cases, the ACS had to weigh the costs of false-positive mammograms. The follow-up to a positive mammogram is often a biopsy; that’s an invasive surgical procedure, and costly. Contrast that with the follow-up to a positive result for open spina bifida/anencephaly: a non-invasive, cheap ultrasound. And unlike an ultrasound, the biopsy is sometimes quite difficult to interpret; you get some diagnoses of cancer when cancer is not present. Those women may go on to receive treatment—chemotherapy, radiation—for cancer that they don’t have. The costs and physical side effects of that are severe.[33] In one study, it was determined that for every life saved by mammography screening, there were 100 women who got false positives (and learned about it after a biopsy) and five women treated for cancer they didn’t have.[34]
The logic of statistical hypothesis testing is relatively clear. What’s not clear is how we ought to apply those relatively straightforward techniques in actual practice. That often involves difficult financial, medical, and moral decisions.
Statistical Inference: Sampling
When we were testing hypotheses, our starting point was knowledge about how traits were distributed among a large population—e.g., hematocrit levels among healthy men. We now ask a pressing question: how do we acquire such knowledge? How do we figure out how things stand with a very large population? The difficulty is that it’s usually impossible to check every member of the population. Instead, we have to make an inference. This inference involves sampling: instead of testing every member of the population, we test a small portion of the population—a sample— and infer from its properties to the properties of the whole. It’s a simple inductive argument:
The sample has property X.
/∴ The general population has property X.
The argument is inductive: the premise does not guarantee the truth of the conclusion; it merely makes it more probable. As was the case in hypothesis testing, we can be precise about the probabilities involved, and our probabilities come from the good-old bell curve.
Let’s take a simple example.[35] Suppose we were trying to discover the percentage of men in the general population; we survey 100 people, and it turns out there are 55 men in our sample. So, the proportion of men in our sample is .55. We’re trying to make an inference from this premise to a conclusion about the proportion of men in the general population. What’s the probability that the proportion of men in the general population is .55? This isn’t exactly the question we want to answer in these sorts of cases, though. Rather, we ask, what’s the probability that the true proportion of men in the general population is in some range on either side of .55? We can give a precise answer to this question; the answer depends on the size of the range you’re considering in a familiar way.
Given that our sample’s proportion of men is .55, it is relatively more likely that the true proportion in the general population is close to that number, less likely that it’s far away. For example, it’s more likely, given the result of our survey, that in fact 50% of the population is men than it is that only 45% are men. And it’s still less likely that only 40% are men. The same pattern holds in the opposite direction: it’s more likely that the true percentage of men is 60% than 65%. Generally speaking, the further away from our survey results we go, the less probable it is that we have the true value for the general population. The drop off in probabilities described takes the form of a bell curve:
Proportion of Men in the Population
|
|
||||||
| .40 | .45 | .50 | .55 | .60 | .65 | .70 |
The standard deviation of .05 is a function of our sample size of 100.[36] We can use the usual confidence intervals—again, with 2 standard deviations, 95.4% being standard practice—to interpret the findings of our survey: we’re pretty sure—to the tune of 95%—that the general population is between 45% and 65% male.
That’s a pretty wide range. Our result is not that impressive (especially considering the fact that we know the actual number is very close to 50%). But that’s the best we can do given the limitations of our survey. The main limitation, of course, was the size of our sample: 100 people just isn’t very many. We could narrow the range within which we’re 95% confident if we increased our sample size; doing so would likely (though not certainly) give us a proportion in our sample closer to the true value of (approximately) .5. The relationship between the sample size and the width of the confidence intervals is a purely mathematical one. As sample size goes up, standard deviation goes down—the curve narrows:
The pattern of reasoning on display in our toy example is the same as that used in sampling generally. Perhaps the most familiar instances of sampling in everyday life are public opinion surveys. Rather than trying to determine the proportion of people in the general population who are men (not a real mystery), opinion pollsters try to determine the proportion of a given population who, say, intend to vote for a certain candidate, or approve of the job the president is doing, or believe in Bigfoot. Pollsters survey a sample of people on the question at hand, and end up with a result: 29% of Americans believe in Bigfoot, for example.[37] But the headline number, as we have seen, doesn’t tell the whole story. 29% of the sample (in this case, about 1,000 Americans) reported believing in Bigfoot; it doesn’t follow with certainty that 29% of the general population (all Americans) have that belief. Rather, the pollsters have some degree of confidence (again, 95% is standard) that the actual percentage of Americans who believe in Bigfoot is in some range around 29%. You may have heard the “margin of error” mentioned in connection with such surveys. This phrase refers to the very range we’re talking about. In the survey about Bigfoot, the margin of error is 3%. That’s the distance from the mean (the 29% found in the sample) and the ends of the two standard-deviation confidence interval—the range in which we’re 95% sure the true value lies. Again, this range is just a mathematical function of the sample size: if the sample size is around 100, the margin of error is about 10% (see the toy example above: 2 SDs = .10); if the sample size is around 400, you get that down to 5%; at 600, you’re down to 4%; at around 1,000, 3%; to get down to 2%, you need around 2,500 in the sample, and to get down to 1%, you need 10,000.[38] So the real upshot of the Bigfoot survey result is something like this: somewhere between 26% and 32% of Americans believe in Bigfoot, and we’re 95% sure that’s the correct range; or, to put it another way, we used a method for determining the true proportion of Americans who believe in Bigfoot that can be expected to determine a range in which the true value actually falls 95% of the time, and the range that resulted from our application of the method on this occasion was 26% – 32%.
That last sentence, we must admit, would make for a pretty lousy newspaper headline (“29% of Americans believe in Bigfoot!” is much sexier), but it’s the most honest presentation of what the results of this kind of sampling exercise actually show. Sampling gives us a range, which will be wider or narrower depending on the size of the sample, and not even a guarantee that the actual value is within that range. That’s the best we can do; these are inductive, not deductive, arguments.
Finally, on the topic of sampling, we should acknowledge than in actual practice, polling is hard. The mathematical relationships between sample size and margin of error/confidence that we’ve noted all hold in the abstract, but real-life polls can have errors that go beyond these theoretical limitations on their accuracy. As the 2016 U.S. presidential election—and the so-called “Brexit” vote in the United Kingdom that same year, and many, many other examples throughout the history of public opinion polling—showed us, polls can be systematically in error. The kinds of facts we’ve been stating—that with a sample size of 600, a poll has a margin of error of 4% at the 95% confidence level—hold only on the assumption that there’s a systematic relationship between the sample and the general population it’s meant to represent; namely, that the sample is representative. A representative sample mirrors the general population; in the case of people, this means that the sample and the general population have the same demographic make-up—same percentage of old people and young people, white people and people of color, rich people and poor people, etc., etc. Polls whose samples are not representative are likely to misrepresent the feature of the population they’re trying to capture. Suppose I wanted to find out what percentage of the U.S. population thinks favorably of Donald Trump. If I asked 1,000 people in, say, rural Oklahoma, I’d get one result; if I asked 1,000 people in midtown Manhattan, I’d get a much different result. Neither of those two samples is representative of the population of the United States as a whole. To get such a sample, I’d have to be much more careful about whom I surveyed. A famous example from the history of public polling illustrates the difficulties here rather starkly: in the 1936 U.S. presidential election, the contenders were Republican Alf Landon of Kansas, and the incumbent President Franklin D. Roosevelt. A (now-defunct) magazine, Literary Digest conducted a poll with 2.4 million (!) participants, and predicted that Landon would win in a landslide. Instead, he lost in a landslide; FDR won the second of his four presidential elections. What went wrong? With a sample size so large, the margin of error would be tiny. The problem was that their sample was not representative of the American population. They chose participants randomly from three sources: (a) their list of subscribers; (b) car registration forms; and (c) telephone listings. The problem with this selection procedure is that all three groups tended to be wealthier than average. This was 1936, during the depths of the Great Depression. Most people didn’t have enough disposable income to subscribe to magazines, let alone have telephones or own cars. The survey therefore over-sampled Republican voters and got a skewed results. Even a large and seemingly random sample can lead one astray. This is what makes polling so difficult: finding representative samples is hard.[39]
Other practical difficulties with polling are worth noting. First, the way your polling question is worded can make a big difference in the results you get. As we discussed in Chapter 2, the framing of an issue—the words used to specify a particular policy or position—can have a dramatic effect on how a relatively uninformed person will feel about it. If you wanted to know the American public’s opinion on whether or not it’s a good idea to tax the transfer of wealth to the heirs of people whose holdings are more than $5.5 million or so, you’d get one set of responses if you referred to the policy as an “estate tax”, a different set of responses if you referred to it as an “inheritance tax”, and a still different set if you called it the “death tax”. A poll of Tennessee residents found that 85% opposed “Obamacare”, while only 16% opposed “Insure Tennessee” (they’re the same thing, of course).[40] Even slight changes in the wording of questions can alter the results of an opinion poll. This is why the polling firm Gallup hasn’t changed the wording of its presidential-approval question since the 1930s. They always ask: “Do you approve or disapprove of the way [name of president] is handling his job as President?” A deviation from this standard wording can produce different results. The polling firm Ipsos found that its polls were more favorable than others’ for the president. They traced the discrepancy to the different way they worded their question, giving an additional option: “Do you approve, disapprove, or have mixed feelings about the way Barack Obama is handling his job as president?”[41] A conjecture: Obama’s approval rating would go down if pollsters included his middle name (Hussein) when asking the question. Small changes can make a big difference.
Another difficulty with polling is that some questions are harder to get reliable data about than others, simply because they involve topics about which people tend to be untruthful. Asking someone whether he approves of the job the president is doing is one thing; asking him whether or not he’s ever cheated on his taxes, say, is quite another. He’s probably not shy about sharing his opinion on the former question; he’ll be much more reluctant to be truthful on the latter (assuming he’s ever fudged things on his tax returns). There are lots of things it would be difficult to discover for this reason: how often people floss, how much they drink, whether or not they exercise, their sexual habits, and so on. Sometimes this reluctance to share the truth about oneself is quite consequential: some experts think that the reason polls failed to predict the election of Donald Trump as president of the United States in 2016 was that some of his supporters were “shy”— unwilling to admit that they supported the controversial candidate.[42] They had no such qualms in the voting booth, however.
Finally, who’s asking the question—and the context in which it’s asked—can make a big difference. People may be more willing to answer questions in the relative anonymity of an online poll, slightly less willing in the somewhat more personal context of a telephone call, and still less forthcoming in a face-to-face interview. Pollsters use all of these methods to gather data, and the results vary accordingly. Of course, these factors become especially relevant when the question being polled is a sensitive one, or something about which people tend not to be honest or forthcoming. To take an example: the best way to discover how often people truly floss is probably with an anonymous online poll. People would probably be more likely to lie about that over the phone, and still more likely to do so in a face-to-face conversation. The absolute worst source of data on that question, perversely, would probably be from the people who most frequently ask it: dentists and dental hygienists. Every time you go in for a cleaning, they ask you how often you brush and floss; and if you’re like most people, you lie, exaggerating the assiduity with which you attend to your dental-health maintenance (“I brush after every meal and floss twice a day, honest.”).
As was the case with hypothesis testing, the logic of statistical sampling is relatively clear. Things get murky, again, when straightforward abstract methods confront the confounding factors involved in real-life application.
EXERCISES
- I and a bunch of my friends are getting ready to play a rousing game of “army men”. Together, we have 110 of the little plastic toy soldiers—enough for quite a battle. However, some of us have more soldiers than others. Will, Brian and I each have 25; Roger and Joe have 11 each; Dan has 4; John and Herb each have 3; Mike, Jamie, and Dennis have only 1 each.
(a) What is the mean number of army men held? What’s the median?
(b) Jamie, for example, is perhaps understandably disgruntled about the distribution; I, on the other hand, am satisfied with the arrangement. In defending our positions, each of us might refer to the “average person” and the number of army men he has. Which sense of ‘average’—mean or median—should Jamie use to gain a rhetorical advantage? Which should sense should I use?
2. Consider cats and dogs—the domesticated kind, pets (tigers don’t count). Suppose I produced a histogram for a very large number of pet cats based on their weight, and did the same for pet dogs. Which distribution would have the larger standard deviation?
3. Men’s heights are normally distributed, with a mean of about 70 inches and a standard deviation of about 3 inches. 68.3% of men fall within what range of heights? Where do 95.4% of them fall? 99.7%? My father-in-law was 76 inches tall. What percentage of men were taller than he was?
4. Women, on average, have lower hematocrit levels than men. The mean for healthy women is 42%, with a standard deviation of 3%. Suppose we want to test the null hypothesis that Alice is healthy. What are the hematocrit readings above which and below which Alice’s test result would be considered significant at the .05 level?
5. Among healthy people, the mean (fasting) blood glucose level is 90 mg/dL, with a standard deviation of 9 mg/dL. What are the levels at the high and low end of the 95.4% confidence interval? Recently, I had my blood tested and got a result of 100 mg/dL. Is this result significant at the .05 level? My result was flagged as being potentially indicative of my being “pre-diabetic” (high blood glucose is a marker for diabetes). My doctor said this is a new standard, since diabetes is on the rise lately, but I shouldn’t worry because I wasn’t overweight and was otherwise healthy. Compared to a testing regime that only flags patients outside the two standard-deviation confidence interval, does this new practice of flagging results at 100 mg/dL increase or decrease the sensitivity of the diabetes screening? Does it increase or decrease its specificity?
6. A stroke is when blood fails to reach a part of the brain because of an obstruction of a blood vessel. Often the obstruction is due to atherosclerosis—a hardening/narrowing of the arteries from plaque buildup. Strokes can be really bad, so it would be nice to predict them. Recent research has sought for a potentially predictive biomarker, and one study found that among stroke victims there was an unusually high level of an enzyme called myeloperoxidase: the mean was 583 pmol/L, with a standard deviation of 48 pmol/L.[43] Suppose we wanted to devise a screening test on the basis of this data. To guarantee that we caught 99.7% of potential stroke victims, what range of myeloperoxidase levels should get a “positive” test result? If the mean level of myeloperoxidase among healthy people is 425 pmol/L, with a standard deviation of 36 pmol/L, approximately what percentage of healthy people will get a positive result from our proposed screening test?
7. I survey a sample of 1,000 Americans (assume it’s representative) and 43% of them report that they believe God created human beings in their present form less than 10,000 years ago.[44] At the 95% confidence level, what is the range within which the true percentage probably lies?
8. Volunteer members of Mothers Against Drunk Driving conducted a door-to-door survey in a college dormitory on a Saturday night, and discovered that students drink and average of two alcoholic beverages per week. What are some reasons to doubt the results of this survey?
V. How to Lie with Statistics[45]
The basic grounding in fundamental statistical concepts and techniques provided in the last section gives us the ability to understand and analyze statistical arguments. Since real-life examples of such arguments are so often manipulative and misleading, our aim in this section is to build on the foundation of the last by examining some of the most common statistical fallacies—the bad arguments and deceptive techniques used to try to bamboozle us with numbers.
Impressive Numbers without Context
I’m considering buying a new brand of shampoo. The one I’m looking at promises “85% more body”. That sounds great to me (I’m pretty bald; I can use all the extra body I can get). But before I make my purchase, maybe I should consider the fact that the shampoo bottle doesn’t answer this simple follow-up question: 85% more body than what? The bottle does mention that the formulation inside is “new and improved”. So maybe it’s 85% more body than the unimproved shampoo? Or possibly they mean that their shampoo gives hair 85% more body than their competitors’. Which competitor, though? The one that does the best at giving hair more body? The one that does the worst? The average of all the competing brands? Or maybe it’s 85% more body than something else entirely. I once had a high school teacher who advised me to massage my scalp for 10 minutes every day to prevent baldness (I didn’t take the suggestion; maybe I should have). Perhaps this shampoo produces 85% more body that daily 10-minute massages. Or maybe it’s 85% more body than never washing your hair at all. And just what is “body” anyway? How is it quantified and measured? Did they take high-precision calipers and systematically gauge the widths of hairs? Or is it more a function of coverage—hairs per square inch of scalp surface area?
The sad fact is, answers to these questions are not forthcoming. The claim that the shampoo will give my hair 85% more body sounds impressive, but without some additional information for me to contextualize that claim, I have no idea what it means. This is a classic rhetorical technique: throw out a large number to impress your audience, without providing the context necessary for them to evaluate whether or not your claim is actually all that impressive. Usually, on closer examination, it isn’t. Advertisers and politicians use this technique all the time.
In the spring of 2009, the economy was in really bad shape (the fallout from the financial crisis that began in the fall of the year before was still being felt; stock market indices didn’t hit their bottom until March 2009, and the unemployment rate was still on the rise). Barack Obama, the newly inaugurated president at the time, wanted to send the message to the American people that he got it: households were cutting back on their spending because of the recession, and so the government would do the same thing.[46] After his first meeting with his cabinet (the Secretaries of Defense, State, Energy, etc.), he held a press conference in which he announced that he had ordered each of them to cut $100 million from their agencies’ budgets. He had a great line to go with the announcement: “$100 million there, $100 million here—pretty soon, even here in Washington, it adds up to real money.” Funny. And impressive-sounding. $100 million is a hell of a lot of money! At least, it’s a hell of a lot of money to me. I’ve got—give me a second while I check—$64 in my wallet right now. I wish I had $100 million. But of course my personal finances are the wrong context in which to evaluate the president’s announcement. He’s talking about cutting from the federal budget; that’s the context. How big is that? In 2009, it was a little more the $3 trillion. There are fifteen departments that the members of the cabinet oversee. The cut Obama ordered amounted to $1.5 billion, then. That’s .05% of the federal budget. That number’s not sounding as impressive now that we put it in the proper context.
2009 provides another example of this technique. Opponents of the Affordable Care Act (“Obamacare”) complained about the length of the bill: they repeated over and over that it was 1,000 pages long. That complaint dovetailed nicely with their characterization of the law as a boondoggle and a government takeover of the healthcare system. 1,000 pages sure sounds like a lot of pages. This book comes in under 250 pages; imagine if it were 1,000! That would be up there with notoriously long books like War and Peace, Les Miserable, and Infinite Jest. It’s long for a book, but is it a lot of pages for a piece of federal legislation? Well, it’s big, but certainly not unprecedented. That year’s stimulus bill was about the same length. President Bush’s 2007 budget bill was just shy of 1,500 pages.[47] His No Child Left Behind bill clocks in at just shy of 700. The fact is, major pieces of legislation have a lot of pages. The Affordable Care Act was not especially unusual.
Misunderstanding Error
As we discussed, built in to the logic of sampling is a margin of error. It is true of measurement generally that random error is unavoidable: whether you’re measuring length, weight, velocity, or whatever, there are inherent limits to the precision and accuracy with which our instruments can measure things. Measurement errors are built in to the logic of scientific practice generally; they must be accounted for. Failure to do so—or intentionally ignoring error—can produce misleading reports of findings.
This is particularly clear in the case of public opinion surveys. As we saw, the results of such polls are not the precise percentages that are often reported, but rather ranges of possible percentages (with those ranges only being reliable at the 95% confidence level, typically). And so to report the results of a survey, for example, as “29% of Americans believe is Bigfoot”, is a bit misleading since it leaves out the margin of error and the confidence level. A worse sin is committed (quite commonly) when comparisons between percentages are made and the margin of error is omitted. This is typical in politics, when the levels of support for two contenders for an office are being measured. A typical newspaper headline might report something like this: “Candidate Sue Surges into the Lead over Incumbent Bob in Latest Poll, 44% to 43%”. This is a sexy headline: it’s likely to sell papers (or, nowadays, generate clicks), both to (happy) Sue supporters and (alarmed) Bob supporters. But it’s misleading: it suggests a level of precision, a definitive result, that the data simply do not support. Let’s suppose that the margin of error for this hypothetical poll was 3%. What the survey results actually tell us, then, is that (at the 95% confidence level) the true level of support for Sue in the general population is somewhere between 41% and 47%, while the true level of support for Bob is somewhere between 40% and 46%. Those data are consistent with a Sue lead, to be sure; but they also allow for a commanding 46% to 41% lead for Bob. The best we can say is that it’s slightly more likely that Sue’s true level of support is higher than Bob’s (at least, we’re pretty sure; 95% confidence interval and all). When differences are smaller than the margin of error (really, twice the margin of error when comparing two numbers), they just don’t mean very much. That’s a fact that headline-writers typically ignore. This gives readers a misleading impression about the certainty with which the state of the race can be known.
Early in their training, scientists learn that they cannot report values that are smaller than the error attached to their measurements. If you weigh some substance, say, and then run an experiment in which it’s converted into a gas, you can plug your numbers into the ideal gas law and punch them into your calculator, but you’re not allowed to report all the numbers that show up after the decimal place. The number of so-called “significant digits” (or sometimes “figures”) you can use is constrained by the size of the error in your measurements. If you can only know the original weight to within .001 grams, for example, then even though the calculator spits out .4237645, you can only report a result using three significant digits—.424 after rounding.
The more significant digits you report, the more precise you imply your measurement is. This can have the rhetorical effect of making your audience easier to persuade. Precise numbers are impressive; they give people the impression that you really know what you’re talking about, that you’ve done some serious quantitative analytical work. Suppose I ask 1,000 college students how much sleep they got last night.[48] I add up all the numbers and divide by 1,000, and my calculator gives me 7.037 hours. If I went around telling people that I’d done a study that showed that the average college student gets 7.037 hours of sleep per night, they’d be pretty impressed: my research methods were so thorough that I can report sleep times down to the thousandths of an hour. They’ve probably got a mental picture of my laboratory, with elaborate equipment hooked up to college students in beds, measuring things like rapid eye movement and breathing patterns to determine the precise instants at which sleep begins and ends. But I have no such laboratory. I just asked a bunch of people. Ask yourself: how much sleep did you get last night? I got about 9 hours (it’s the weekend). The key word in that sentence is ‘about’. Could it have been a little bit more or less than 9 hours? Could it have been 9 hours and 15 minutes? 8 hours and 45 minutes? Sure. The error on any person’s report of how much they slept last night is bound to be something like a quarter of an hour. That means that I’m not entitled to those 37 thousandths of an hour that I reported from my little survey. The best I can do is say that the average college student gets about 7 hours of sleep per night, plus or minus 15 minutes or so. 7.037 is precise, but the precision of that figure is spurious (not genuine, false).
Ignoring the error attached to measurements can have profound real-life effects. Consider the 2000 U.S. presidential election. George W. Bush defeated Al Gore that year, and it all came down to the state of Florida, where the final margin of victory (after recounts were started, then stopped, then started again, then finally stopped by order of the Supreme Court of the United States) was 327 votes. There were about 6 million votes cast in Florida that year. The margin of 327 is about .005% of the total. Here’s the thing: counting votes is a measurement like any other; there is an error attached to it. You may remember that in many Florida counties, they were using punch-card ballots, where voters indicate their preference by punching a hole through a perforated circle in the paper next to their candidate’s name. Sometimes, the circular piece of paper—a so-called “chad”—doesn’t get completely detached from the ballot, and when that ballot gets run through the vote-counting machine, the chad ends up covering the hole and a non-vote is mistakenly registered. Other types of vote-counting methods—even hand-counting[49]—have their own error. And whatever method is used, the error is going to be greater than the .005% margin that decided the election. As one prominent mathematician put it, “We’re measuring bacteria with a yardstick.”[50] That is, the instrument we’re using (counting, by machine or by hand) is too crude to measure the size of the thing we’re interested in (the difference between Bush and Gore). He suggested they flip a coin to decide Florida. It’s simply impossible to know who won that election.
In 2011, newly elected Wisconsin Governor Scott Walker, along with his allies in the state legislature, passed a budget bill that had the effect, among other things, of cutting the pay of public sector employees by a pretty significant amount. There was a lot of uproar; you may have seen the protests on the news. People who were against the bill made their case in various ways. One of the lines of attack was economic: depriving so many Wisconsin residents of so much money would damage the state’s economy and cause job losses (state workers would spend less, which would hurt local businesses’ bottom lines, which would cause them to lay off their employees). One newspaper story at the time quoted a professor of economics who claimed that the Governor’s bill would cost the state 21,843 jobs.[51] Not 21, 844 jobs; it’s not that bad. Only 21,843. This number sounds impressive; it’s very precise. But of course that precision is spurious. Estimating the economic effects of public policy is an extremely uncertain business. I don’t know what kind of model this economist was using to make his estimate, but whatever it was, it’s impossible for its results to be reliable enough to report that many significant digits. My guess is that at best the 2 in 21,843 has any meaning at all.
Tricky Percentages
Statistical arguments are full of percentages, and there are lots of ways you can fool people with them. The key to not being fooled by such figures, usually, is to keep in mind what it’s a percentage of. Inappropriate, shifting, or strategically chosen numbers can give you misleading percentages.
When the numbers are very small, using percentages instead of fractions is misleading. Johns Hopkins Medical School, when it opened in 1893, was one of the few medical schools that allowed women to matriculate.[52] In those benighted times, people worried about women enrolling in schools with men for a variety of silly reasons. One of them was the fear that the impressionable young ladies would fall in love with their professors and marry them. Absurd, right? Well, maybe not: in the first class to enroll at the school, 33% of the women did indeed marry their professors! The sexists were apparently right. That figure sounds impressive, until you learn that the denominator is 3. Three women enrolled at Johns Hopkins that first year, and one of them married her anatomy professor. Using the percentage rather than the fraction exaggerates in a misleading way. Another made up example: I live in a relatively safe little town. If I saw a headline in my local newspaper that said “Armed Robberies are Up 100% over Last Year” I would be quite alarmed. That is, until I realized that last year there was one armed robbery in town, and this year there were two. That is a 100% increase, but using the percentage of such a small number is misleading.
You can fool people by changing the number you’re taking a percentage of mid-stream. Suppose you’re an employee at my aforementioned LogiCorp. You evaluate arguments for $10.00 per hour. One day, I call all my employees together for a meeting. The economy has taken a turn for the worse, I announce, and we’ve got fewer arguments coming in for evaluation; business is slowing. I don’t want to lay anybody off, though, so I suggest that we all share the pain: I’ll cut everybody’s pay by 20%; but when the economy picks back up, I’ll make it up to you. So you agree to go along with this plan, and you suffer through a year of making a mere $8.00 per hour evaluating arguments. But when the year is up, I call everybody together and announce that things have been improving and I’m ready to set things right: starting today, everybody gets a 20% raise. First a 20% cut, now a 20% raise; we’re back to where we were, right? Wrong. I changed numbers midstream. When I cut your pay initially, I took twenty percent of $10.00, which is a reduction of $2.00. When I gave you a raise, I gave you twenty percent of your reduced pay rate of $8.00 per hour. That’s only $1.60. Your final pay rate is a mere $9.60 per hour.[53]
Often, people make a strategic decision about what number to take a percentage of, choosing the one that gives them a more impressive-sounding, rhetorically effective figure. Suppose I, as the CEO of LogiCorp, set an ambitious goal for the company over the next year: I propose that we increase our productivity from 800 arguments evaluated per day to 1,000 arguments per day. At the end of the year, we’re evaluating 900 arguments per day. We didn’t reach our goal, but we did make an improvement. In my annual report to investors, I proclaim that we were 90% successful. That sounds good; 90% is really close to 100%. But it’s misleading. I chose to take a percentage of 1,000: 900 divided by 1,000 give us 90%. But is that the appropriate way to measure the degree to which we met the goal? I wanted to increase our production from 800 to 1,000; that is, I wanted a total increase of 200 arguments per day. How much of an increase did we actually get? We went from 800 up to 900; that’s an increase of 100. Our goal was 200, but we only got up to 100. In other words, we only got to 50% of our goal. That doesn’t sound as good.
Another case of strategic choices. Opponents of abortion rights might point out that 97% of gynecologists in the United States have had patients seek abortions. This creates the impression that there’s an epidemic of abortion-seeking, that it happens regularly. Someone on the other side of the debate might point out that only 1.25% of women of childbearing age get an abortion each year. That’s hardly an epidemic. Each of the participants in this debate has chosen a convenient number to take a percentage of. For the anti-abortion activist, that is the number of gynecologists. It’s true that 97% have patients who seek abortions; only 14% of them actually perform the procedure, though. The 97% exaggerates the prevalence of abortion (to achieve a rhetorical effect). For the pro-choice activist, it is convenient to take a percentage of the total number of women of childbearing age. It’s true that a tiny fraction of them get abortions in a given year; but we have to keep in mind that only a small percentage of those women are pregnant in a given year. As a matter of fact, among those that actually get pregnant, something like 17% have an abortion. The 1.25% minimizes the prevalence of abortion (again, to achieve a rhetorical effect).
The Base-Rate Fallacy
The base rate is the frequency with which some kind of event occurs, or some kind of phenomenon is observed. When we ignore this information, or forget about it, we commit a fallacy and make mistakes in reasoning.
Most car accidents occur in broad daylight, at low speeds, and close to home. So does that mean I’m safer if I drive really fast, at night, in the rain, far away from my house? Of course not. Then why are there more accidents in the former conditions? The base rates: much more of our driving time is spent at low speeds, during the day, and close to home; relatively little of it is spent driving fast at night, in the rain and far from home.[54]
Consider a woman formerly known as Mary (she changed her name to Moon Flower). She’s a committed pacifist, vegan, and environmentalist; she volunteers with Green Peace; her favorite exercise is yoga. Which is more probable: that she’s a best-selling author of new-age, alternative-medicine, self-help books—or that she’s a waitress? If you answered that she’s more likely to be a best-selling author of self-help books, you fell victim to the base-rate fallacy. Granted, Moon Flower fits the stereotype of the kind of person who would be the author of such books perfectly. Nevertheless, it’s far more probable that a person with those characteristics would be a waitress than a best-selling author. Why? Base rates. There are far, far (far!) more waitresses in the world than best-selling authors (of new-age, alternative-medicine, self-help books). The base rate of waitressing is higher than that of best-selling authorship by many orders of magnitude.
Suppose there’s a medical screening test for a serious disease that is very accurate: it only produces false positives 1% of the time, and it only produces false negatives 1% of the time (it’s highly sensitive and highly specific). The disease is serious, but rare: it only occurs in 1 out of every 100,000 people. Suppose you get screened for this disease and your result is positive; that is, you’re flagged as possibly having the disease. Given what we know, what’s the probability that you’re actually sick? It’s not 99%, despite the accuracy of the test. It’s much lower. And I can prove it, using our old friend Bayes’ Law. The key to seeing why the probability is much lower than 99%, as we shall see, is taking the base rate of the disease into account.
There are two hypotheses to consider: that you’re sick (call it ‘S’) and that you’re not sick (~ S). The evidence we have is a positive test result (P). We want to know the probability that you’re sick, given this evidence: P(S | P). Bayes’ Law tells us how to calculate this:
P(S) x P(P | S)
P(S | P) = ———————————————–
P(S) x P(P | S) + P(~ S) x P(P | ~ S)
The base rate of the sickness is the rate at which it occurs in the general population. It’s rare: it only occurs in 1 out of 100,000 people. This number corresponds to the prior probability for the sickness in our formula—P(S). We have to multiply in the numerator by 1/100,000; this will have the effect of keeping down the probability of sickness, even given the positive test result. What about the other terms in our equation? ‘P(~ S)’ just picks out the prior probability of not being sick; if P(S) = 1/100,000, then P(~ S) = 99,999/100,000. ‘P(P | S)’ is the probability that you would get a positive test result, assuming you were in fact sick. We’re told that the test is very accurate: it only tells sick people that they’re healthy 1% of the time (1% rate of false negatives); so the probability that a sick person would get a positive test result is 99%—P(P | S) = .99. ‘P(P | ~ S)’ is the probability that you’d get a positive result if you weren’t sick. That’s the rate of false positives, which is 1%— P(P | ~ S) = .01. Plugging these numbers into the formula, we get the result that P(S | P) = .000999. That’s right, given a positive result from this very-accurate screening test, you’re probability of being sick is just under 1/10,000. The test is accurate, but the disease is so rare (its base rate is so low) that your chances of being sick are still very low even after a positive result.
Sometimes people will ignore base rates on purpose to try to fool you. Did you know that marijuana is more dangerous than heroin? Neither did I. But look at this chart:
That graphic published in a story in USA Today under the headline “Marijuana poses more risks than many realize.”[55] The chart/headline combo create an alarming impression: if so many more people are going to the emergency room because of marijuana, it must be more dangerous than I realized. Look at that: more than twice as many emergency room visits for pot than heroin; it’s almost as bad as cocaine! Or maybe not. What this chart ignores is the base rates of marijuana-, cocaine-, and heroin-use in the population. Far (far!) more people use marijuana than use heroin or cocaine. A truer measure of the relative dangers of the various drugs would be the number of emergency room visits per user. That gives you a far different chart:[56]
Lying with Pictures
Speaking of charts, they are another tool that can be used (abused) to make dubious statistical arguments. We often use charts and other pictures to graphically convey quantitative information. But we must take special care that our pictures accurately depict that information. There are all sorts of ways in which graphical presentations of data can distort the actual state of affairs and mislead our audience.
Consider, once again, my fictional company, LogiCorp. Business has been improving lately, and I’m looking to get some outside investors so I can grow even more quickly. So I decide to go on that TV show Shark Tank. You know, the one with Mark Cuban and panel of other rich people, where you make a presentation to them and they decide whether or not your idea is worth investing in. Anyway, I need to plan a persuasive presentation to convince one of the sharks to give me a whole bunch of money for LogiCorp. I’m going to use a graph to impress them with company’s potential for future growth. Here’s a graph of my profits over the last decade:
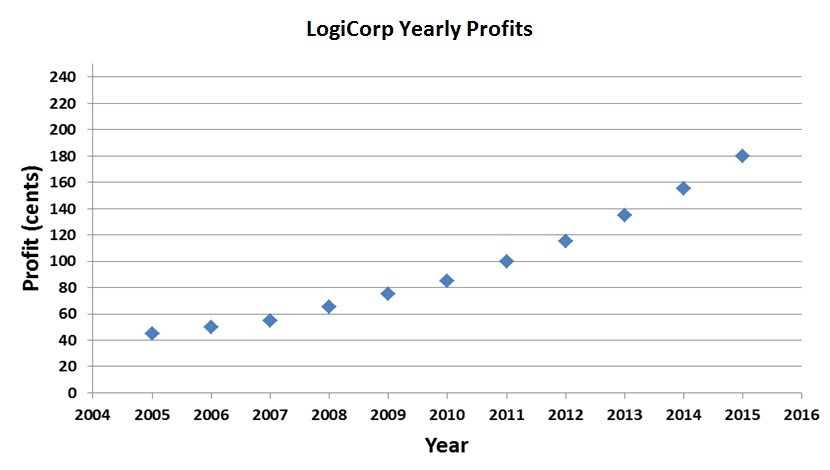
Not bad. But not great, either. The positive trend in profits is clearly visible, but it would be nice if I could make it look a little more dramatic. I’ll just tweak things a bit:
Better. All I did was adjust the y-axis. No reason it has to go all the way down to zero and up to 240. Now the upward slope is accentuated; it looks like LogiCorp is growing more quickly. But I think I can do even better. Why does the x-axis have to be so long? If I compressed the graph horizontally, my curve would slope up even more dramatically:
Now that’s explosive growth! The sharks are gonna love this. Well, that is, as long as they don’t look too closely at the chart. Profits on the order of $1.80 per year aren’t going to impress a billionaire like Mark Cuban. But I can fix that:
There. For all those sharks know, profits are measure in the millions of dollars. Of course, for all my manipulations, they can still see that profits have increased 400% over the decade. That’s pretty good, of course, but maybe I can leave a little room for them to mentally fill in more impressive numbers:
That’s the one. Soaring profits, and it looks like they started close to zero and went up to—well, we can’t really tell. Maybe those horizontal lines go up in increments of 100, or 1,000. LogiCorp’s profits could be unimaginably high.
People manipulate the y-axis of charts for rhetorical effect all the time. In their “Pledge to America” document of 2010, the Republican Party promised to pursue various policy priorities if they were able to achieve a majority in the House of Representatives (which they did). They included the following chart in that diagram to illustrate that government spending was out of control:
Writing for New Republic, Alexander Hart pointed out that the Republicans’ graph, by starting the y-axis at 17% and only going up to 24%, exaggerates the magnitude of the increase. That bar on the right is more than twice as big as the other two, but federal spending hadn’t doubled. He produced the following alternative presentation of the data[57]:
Writing for The Washington Post, liberal blogger Ezra Klein passed along the original graph and the more “honest” one. Many of his commenters (including your humble author) pointed out that the new graph was an over-correction of the first: it minimizes the change in spending by taking the y-axis all the way up to 100. He produced a final graph that’s probably the best way to present the spending data[58]:
One can make mischief on the x-axis, too. In an April 2011 editorial entitled “Where the Tax Money Is”, The Wall Street Journal made the case that President Obama’s proposal to raise taxes on the rich was a bad idea.[59] If he was really serious about raising revenue, he would have to raise taxes on the middle class, since that’s where most of the money is. To back up that claim, they produced this graph:
This one is subtle. What they present has the appearance of a histogram, but it breaks one of the rules for such charts: each of the bars has to represent the same portion of the population. That’s not even close to the case here. To get their tall bars in the middle of the income distribution, the Journal’s editorial board groups together incomes between $50 and $75 thousand, $75 and $100 thousand, then $100 and $200 thousand, and so on. There are far (far!) more people (or probably households; that’s how these data are usually reported) in those income ranges than there are in, say, the range between $20 and $25 thousand, or $5 to $10 million—and yet those ranges get their own bars, too. That’s just not how histograms work. Each bar in an income distribution chart would have to contain the same number of people (or households). When you produce such a histogram, you see what the distribution really looks like (these data are from a different tax year, but the basic shape of the graph didn’t change during the interim):
Using The Wall Street Journal’s method of generating histograms—where each bar can represent any number of different households—you can “prove” anything you like. It’s not the rich or even the middle class we should go after if we really want to raise revenue; it’s the poor. That’s where the money is:
There are other ways besides charts and graphs to visually present quantitative information: pictograms. There’s a sophisticated and rule-based method for representing statistical information using such pictures. It was pioneered in the 1920s by the Austrian philosopher Otto Neurath, and was originally called the Vienna Method of Pictorial Statistics (Wiener Methode der Bildstatistik); eventually it came to be known as Isotype (International System of TYpographic Picture Education)[60]. The principles of Neurath’s system were such as to prevent the misrepresentation of data with pictograms. Perhaps the most important rule is that greater quantities are to be represented not by larger pictures, but by greater numbers of same-sized pictures. So, for instance, if I wanted to represent the fact that domestic oil production in the United States has doubled over the past several years, I could use the following depiction[61]:



THEN NOW
It would be misleading to flout Neurath’s principles and instead represent the increase with a larger barrel:


THEN NOW
All I did was double the size of the image. But I doubled it in both dimensions: it’s both twice as wide and twice as tall. Moreover, since oil barrels are three dimensional objects, I’ve also depicted a barrel on the right that’s twice as deep. The important thing about oil barrels is how much oil they can hold—their volume. By doubling the barrel in all three dimensions, I’ve depicted a barrel on the right that can hold 8 times as much oil as the one on the left. What I’m showing isn’t a doubling of oil production; it’s an eight-fold increase.
Alas, people break Neurath’s rules all the time, and end up (intentionally or not) exaggerating the phenomena they’re trying to depict. Matthew Yglesias, writing in Architecture magazine, made the point that the housing “bubble” that reached full inflation in 2006 (when lots of homes were built) was not all that unusual. If you look at recent history, you see similar cycles of boom and bust, with periods of lots of building followed by periods of relatively little. The magazine produced a graphic to present the data on home construction, and Yglesias made a point to post it on his blog at Slate.com because he thought it was illustrative.[62] Here’s the graphic:
It’s a striking figure, but it exaggerates the swings it’s trying to depict. The picograms are scaled to the numbers in the little houses (which represent the number of homes built in the given months), but in both dimensions. And of course houses are three-dimensional objects, so that even though the picture doesn’t depict the third dimension, our unconscious mind knows that these little domiciles have volume. So the Jan. 2006 house (2,273) is more than five times wider and higher than the April 2009 house (478). But five times in three dimensions: 5 x 5 x 5 = 125. The Jan. 2006 house is over 125 times larger than the April 2009 house; that’s why it looks like we have a mansion next to a shed. There were swings in housing construction over the years, but they weren’t as large as this graphic makes them seem.
One ubiquitous picture that’s easy to misinterpret, not because anybody broke Neurath’s rules, but simply because of how things happen to be in the world, is the map of the United States. What makes it tricky is that the individual states’ sizes are not proportional to their populations. This has the effect of exaggerating certain phenomena. Consider the final results of the 2016 presidential election, pictured, as they normally are, with states that went for the Republican candidate in red and those that went for the Democrat in blue. This is what you get[63]:
Look at all that red! Clinton apparently got trounced. Except she didn’t: she won the popular vote by more than three million. It looks like there are a lot more Trump votes because he won a lot of states that are very large but contain very few voters. Those Great Plains states are huge, but hardly anybody lives up there. If you were to adjust the map, making the states’ sizes proportional to their populations, you’d end up with something like this[64]:
And this is only a partial correction: this sizes the states by electors in the Electoral College; that still exaggerates the sizes of some of those less-populated states. A true adjustment would have to show more blue than red, since Clinton won more votes overall.
I’ll finish with an example stolen directly from the inspiration for this section—Darrell Huff’s How to Lie with Statistics.[65] It is a map of the United States made to raise alarm over the amount of spending being done by the federal government (it was produced over half a century ago; some things never change). Here it is:
The Darkening Shadow
Federal Spending = Incomes of All People in Shaded States
That makes it look like federal spending is the equivalent of half the country’s incomes! But Huff produced his own map (“Eastern style”), shading different states, same total population:
Not nearly so alarming.
People try to fool you in so many different ways. The only defense is a little logic, and a whole lot of skepticism. Be vigilant!
- Don’t freak out about the word ‘calculus’. We’re not doing derivatives and integrals here; we’re using that word in a generic sense, as in ‘a system for performing calculations’, or something like that. Also, don’t get freaked out about ‘mathematics’. This is really simple, fifth-grade stuff: adding and multiplying fractions and decimals. ↵
- Twain attributes the remark to British Prime Minister Benjamin Disraeli, though it’s not really clear who said it first. ↵
- If you think otherwise, you’re committing what’s known as the Gambler’s Fallacy. It’s surprisingly common. Go to a casino and you’ll see people committing it. Head to the roulette wheel, for example, where people can bet on whether the ball lands in a red or a black space. After a run of say, five reds in a row, somebody will commit the fallacy: “Red is hot! I’m betting on it again.” This person believes that the results of the previous spins somehow affect the probability of the outcome of the next one. But they don’t. Notice that an equally compelling (and fallacious) case can be made for black: “Five reds in a row? Black is due. I’m betting on black.” ↵
- A standard deck has 52 playing cards, equally divided among four suits (hearts, diamonds, clubs, and spades) with 13 different cards in each suit: Ace (A), 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack (J), Queen (Q), and King (K). ↵
- This makes good sense. If you throw a coin twice, there are four distinct ways things could go: (1) you throw heads twice; (2) you throw heads the first time, tails the second; (3) you throw tails the first time, heads the second; (4) you throw tails twice. In three out of those four scenarios (all but the last), you’ve thrown at least one head. ↵
- Really: http://mentalfloss.com/article/62593/how-doesjellybellycreateitsweirdflavors ↵
- Inspired by an exercise from Copi and Cohen, pp. 596 - 597 ↵
- In this and what follows, I am indebted to Copi and Cohen’s presentation for inspiration. ↵
- It’s more complicated than this, but we’re simplifying to make things easier. ↵
- They’re insured through the FDIC—Federal Deposit Insurance Corporation—created during the Great Depression to prevent bank runs. Before this government insurance on deposits, if people thought a bank was in trouble, everybody tried to withdraw their money at the same time; that’s a “bank run”. Think about the scene in It’s a Wonderful Life when George is about to leave on his honeymoon, but he has to go back to the Bailey Building and Loan to prevent such a catastrophe. Anyway, if everybody knows they'll get their money back even if the bank goes under, such things won't happen; that's what the FDIC is for. ↵
- Unless, of course, the federal government goes out of business. But in that case, $1,000 might not be too useful anyway ↵
- This function maps 1 unit of wealth to 10 units of utility (never mind what those units are). 2 units of wealth produces 30 units of utility, and so on: 3 – 48; 4 – 60; 5 – 70; 6 – 78; 7 – 84; 8 – 90; 9 – 96; 10 – 100. This mapping comes from Daniel Kahneman, 2011, Thinking, Fast and Slow, New York: Farrar, Strauss, and Giroux, p. 273. ↵
- For this and many other examples, see Kahneman 2011. 18 Again, see Kahneman 2011 for details. ↵
- Again, see Kahneman 2011 for details. ↵
- There’s a whole literature on this. See this article for an overview: Hájek, Alan, "Interpretations of Probability", The Stanford Encyclopedia of Philosophy (Winter 2012 Edition), Edward N. Zalta (ed.), URL = <https://plato.stanford.edu/archives/win2012/entries/probability-interpret/>. ↵
- It’s easy to derive this theorem, starting with the general product rule. We know P(E • H) = P(E) x P(H | E), no matter what ‘E’ and ‘H’ stand for. A little algebraic manipulation gives us P(H | E) = P(E • H) / P(E). It’s a truth of logic that the expression ‘E • H’ is equivalent to ‘H • E’, so we can replace ‘P(E • H)’ with ‘P(H • E)’ in the numerator. And again, by the general product rule, P(H • E) = P(H) x P(E | H)—our final numerator. ↵
- Provided you set things up carefully. Check out this video: https://www.youtube.com/watch?v=E43-CfukEgs. ↵
- Or, it is travelling a straight line, just through a space that is curved. Same thing. ↵
- I know. In the example, maybe it’s the cold weather and the new detergent causing my rash. Let’s set that possibility aside. ↵
- We add the subscript ‘k’ to the hypothesis we’re entertaining, and stipulate the k is between 1 and n simply to ensure that the hypothesis in question is among the set of exhaustive, mutually exclusive possibilities H1, H2, …, Hn. ↵
- Inspiration for this example, as with much that follows, comes from Darrell Huff, 1954, How to Lie with Statistics, New York: Norton. ↵
- In 2014, the richest fifth of American households accounted for over 51% of income; the poorest fifth, 3%. ↵
- “Gaussian” because the great German mathematician Carl Friedrich Gauss made a study of such distributions in the early 19th century (in connection with their relationship to errors in measurement). ↵
- This is a consequence of a mathematical result, the Central Limit Theorem, the basic upshot of which is that if some random variable (a trait like IQ, for example, to be concrete) is the sum of many independent random variables (causes of IQ differences: lots of different genetic factors, lots of different environmental factors), then the variable (IQ) will be normally distributed. The mathematical theorem deals with abstract numbers, and the distribution is only perfectly “normal” when the number of independent variables approaches infinity. That’s why real-life distributions are only approximately normal. ↵
- This is an exaggeration, of course, but not much of one. The average high in San Diego in January is 65°; in July, it’s 75°. Meanwhile, in Milwaukee, the average high in January is 29°, while in July it’s 80°. ↵
- Pick a person at random. How confident are you that they have an IQ between 70 and 130? 95.4%, that’s how confident. ↵
- As a matter of fact, in current practice, other confidence intervals are more often used: 90%, (exactly) 95%, 99%, etc. These ranges lie on either side of the mean within non-whole-number multiples of the standard deviation. For example, the exactly-95% interval is 1.96 SDs to either side of the mean. The convenience of calculators and spreadsheets to do our math for us makes these confidence intervals more practical. But we’ll stick with the 68.3/95.4/99.7 intervals for simplicity’s sake. ↵
- Again, the actual distribution may not be normal, but we will assume that it is in our examples. The basic patterns of reasoning are similar when dealing with different kinds of distributions. ↵
- Actually, the typical level is now exactly 95%, or 1.96 standard deviations from the mean. From now on, we’re just going to pretend that the 95.4% and 95% levels are the same thing. ↵
- Picture from a post at www.pregnancylab.net by David Grenache, PhD: http://www.pregnancylab.net/2012/11/screening-forneuraltubedefects.html ↵
- False positive: the baby was perfectly healthy. ↵
- Except for those known to be at risk, who should start earlier. ↵
- Especially perverse are the cases in which the radiation treatment itself causes cancer in a patient who didn’t have to be treated to begin with. ↵
- PC Gøtzsche and KJ Jørgensen, 2013, Cochrane Database of Systematic Reviews (6), CD001877.pub5 ↵
- I am indebted for this example in particular (and for much background on the presentation of statistical reasoning in general) to John Norton, 1998, How Science Works, New York: McGraw-Hill, pp. 12.14 – 12.15. ↵
- And the mean (our result of .55). The mathematical details of the calculation needn’t detain us. ↵
- Here’s an actual survey with that result: http://angusreidglobal.com/wp-content/uploads/2012/03/2012.03.04_Myths.pdf ↵
- Interesting mathematical fact: these relationships hold no matter how big the general population from which you’re sampling (as long as it’s above a certain threshold). It could be the size of the population of Wisconsin or the population of China: if your sample is 600 Wisconsinites, your margin of error is 4%; if it’s 600 Chinese people, it’s still 4%. This is counterintuitive, but true—at least, in the abstract. We’re omitting the very serious difficulty that arises in actual polling (which we will discuss anon): finding the right 600 Wisconsinites or Chinese people to make your survey reliable; China will present more difficulty than Wisconsin. ↵
- It’s even harder than this paragraph makes it out to be. It’s usually impossible for a sample—the people you’ve talked to on the phone about the president or whatever—to mirror the demographics of the population exactly. So pollsters have to weight the responses of certain members of their sample more than others to make up for these discrepancies. This is more art than science. Different pollsters, presented with the exact same data, will make different choices about how to weight things, and will end up reporting different results. See this fascinating piece for an example: http://www.nytimes.com/interactive/2016/09/20/upshot/the-errorthepollingworldrarelytalksabout.html?_r=0 ↵
- Source: http://www.nbcnews.com/politics/elections/rebuke-tennesseegovernorkochgroupshowsitspowern301031 -overnorkochgroupshowsitspowern301031 governorochgroupshowsitspowern301031 ↵
- http://spotlight.ipsos-na.com/index.php/news/ispresidentobamaupordowntheeffectofquestionwordingonlevelsofpresidentialsupport/ ↵
- See here, for example: https://www.washingtonpost.com/news/monkey-cage/wp/2016/12/13/whythepollsmissedin2016wasitshytrumpsupportersafterall/?utm_term=.f20212063a9c ↵
- See this study: https://www.ncbi.nlm.nih.gov/pubmed/21180247 ↵
- See this survey: http://www.gallup.com/poll/27847/Majority-RepublicansDoubtTheoryEvolution.aspx -oubtTheoryEvolution.aspx ↵
- The title of this section, a lot of the topics it discusses, and even some of the examples it uses, are taken from Huff 1954. ↵
- This sounds good, but it’s bad macroeconomics. Most economists agree that during a downturn like that one, the government should borrow and spend more, not less, in order to stimulate the economy. The president knew this; he ushered a huge government spending bill through Congress (The American Reinvestment and Recovery Act) later that year. ↵
- This is a useful resource: http://www.slate.com/articles/news_and_politics/explainer/2009/08/paper_weight.html ↵
- This example inspired by Huff 1954, pp. 106 - 107. ↵
- It may be as high as 2% for hand-counting! See here: https://www.sciencedaily.com/releases/2012/02/120202151713.htm ↵
- John Paulos, “We’re Measuring Bacteria with a Yardstick,” November 22, 2000, The New York Times. ↵
- Steven Verburg, “Study: Budget Could Hurt State’s Economy,” March 20, 2011, Wisconsin State Journal. ↵
- Not because the school’s administration was particularly enlightened. They could only open with the financial support of four wealthy women who made this a condition for their donations. ↵
- This example inspired by Huff 1954, pp. 110 - 111. ↵
- This example inspired by Huff 1954, pp. 77 - 79. ↵
- Liz Szabo, “Marijuana poses more risks than many realize,” July 27, 2014, USA Today. http://www.usatoday.com/story/news/nation/2014/07/27/risks-ofmarijuana/10386699/?sf29269095=1 ↵
- From German Lopez, “Marijuana sends more people to the ER than heroin. But that's not the whole story.” August 2, 2014, Vox.com. http://www.vox.com/2014/8/2/5960307/marijuana-legalizationheroinUSAToday ↵
- Alexander Hart, “Lying With Graphs, Republican Style (Now Featuring 50% More Graphs),” December 22, 2010, New Republic. https://newrepublic.com/article/77893/lying-graphsrepublicanstyle ↵
- Ezra Klein, “Lies, damn lies, and the 'Y' axis,” September 23, 2010, The Washington Post. http://voices.washingtonpost.com/ezra-klein/2010/09/lies_damn_lies_and_the_y_axis.html ↵
- See here: http://www.wsj.com/articles/SB10001424052748704621304576267113524583554 ↵
- See here: https://en.wikipedia.org/wiki/Isotype_(picture_language) ↵
- I’ve been using this example in class for years, and something tells me I got it from somebody else’s book, but I’ve looked through all the books on my shelves and can’t find it. So maybe I made it up myself. But if I didn’t, this footnote acknowledges whoever did. (If you’re that person, let me know!) ↵
- See here: http://www.slate.com/blogs/moneybox/2011/12/23/america_s_housing_shortage.html ↵
- Source of image: https://en.wikipedia.org/wiki/Electoral_College_(United_States) ↵
- Ibid. ↵
- p. 103. ↵